 |
The Left Hand of the Electron |
10 - EUCLID'S FIFTH
Some of my articles stir up more reader comment than others,
and one of the most effective in this respect was one I once wrote in which
I listed those who, in my opinion, were scientists of the first magnitude
and concluded by working up a personal list of the ten greatest scientists
of all time.
Naturally, I received letters arguing for the omission of one or more of
my ten best in favor of one or more others, and I still get them, even now,
seven and a half years after the article was written.
Usually, I reply by explaining that estimates as to the ten greatest scientists
(always excepting the case of
Isaac Newton, concerning whom there can be no
reasonable disagreement) are largely a subjective matter and cannot really
be argued out.
Recently, I received a letter from a reader who argued
that Archimedes, one of my ten, ought to
be replaced by Euclid, who
was not one of my ten. I replied in my usual placating manner, but then went
on to say that Euclid was 'merely a systematizer' while Archimedes had made
very important advances in physics and mathematics.
But later my conscience grew active. I still adhered to my own opinion of
Archimedes taking pride of place over Euclid, but the phase 'merely a
systematizer' bothered me. There is nothing necessarily 'mere' about being
a systematizer.[Sometimes there is. In all my non-fiction writings I am 'merely'
a systematizer. - Just in case you think I'm never modest.]
For three centuries before Euclid (who flourished about 300 B.C.) Greek geometers
had labored at proving one geometric theorem or another and a great many
had been worked out.
What Euclid did was to make a system out of it all. He began with certain
definitions and assumptions and then used them to prove a few theorems. Using
those definitions and assumptions plus the few theorems he had already proved,
he proved a few additional theorems and so on, and so on.
He was the first, as far as we know, to build an elaborate mathematical system
based on the explicit attitude that it was useless to try to prove everything;
that it was essential to make a beginning with some things that could not
be proved but that could be accepted without proof
because they satisfied intuition. Such intuitive
assumptions, without proof, are called 'axioms'.
This was in itself a great intellectual advance, but Euclid did something
more. He picked good axioms. To see what this means, consider that you would
want your list of axioms to be complete, that is, they should suffice to
prove all the theorems that are useful in the particular field of knowledge
being studied. On the other hand they shouldn't be redundant You don't want
to be able to prove all those theorems even after you have omitted one or
more of your axioms from the list; or to be able to prove one or more of
your axioms by the use of the remaining axioms. Finally, your axioms must
be consistent. That is, you do not want to use some axioms to prove that
something is so and then use other axioms to prove the same thing to be
not so.
For two thousand years, Euclid's axiomatic system stood the test. No one
ever found it necessary to add another axiom, and no one was ever able to
eliminate one or to change it substantially - which is a pretty good testimony
to Euclid's judgment. By the end of the nineteenth century, however, when
notions of mathematical rigor had hardened, it was realized that there were
many tacit assumptions in the Euclidean system; that is, assumptions that
Euclid made without specifically saying that he had made them, and that all
his readers also made, apparently without specifically saying so to themselves.
For instance, among his early theorems are several that demonstrate two triangles
to the congruent (equal in both shape and size) by a course of proof that
asks people to imagine that one triangle is moved in space so that it is
superimposed on the other. -That, however, presupposes that a geometrical
figure doesn't change in shape and size when it moves. Of course it doesn't,
you say. Well, you assume it doesn't and I assume it doesn't and
Euclid
assumed it doesn't - but Euclid never said he assumed it.
Again, Euclid assumed that a straight line could extend infinitely in both
directions but never said he was making that assumption. Furthermore, he
never considered such important basic properties as the order of points
in a line, and some of his basic definitions were inadequate-
But never mind. In the last century, Euclidean geometry has been placed on
a basis of the utmost rigor and while that meant the system of axioms and
definitions was altered, Euclid's geometry remained the same. It just meant
that Euclid's axioms and definitions, plus his unexpressed assumptions,
were adequate to the job.
Let's consider Euclid's axioms now. There were ten of them
and he divided them into two groups of five. One group of five was called
'common notions' because they were common to all sciences:
(1) Things which are equal to the same thing are also equal to one
another.
(2) If equals are added to equals, the sums are equal.
(3) If equals are subtracted from equals, the remainders are equal.
(4) Things which coincide with one another are equal to one another.
(5) The whole is greater than the part.
These 'common notions' seem so common, indeed so obvious, so immediately
acceptable by intuition, so incapable of contradiction, that they seem to
represent absolute truth. They seem something a person could seize upon as
soon as he had evolved the light of reason. Without ever sensing the universe
in any way, but living only in the luminous darkness of his own mind, he
would see that things equal to the same thing are equal to one another and
all the rest.
He might then, using Euclid's axioms, work out all the theorems of geometry
and, therefore, the basic properties of the universe from first principles,
without having observed anything.
The Greeks were so fascinated with this notion that all mathematical knowledge
comes from within that they lost one important urge that might have led to
the development of experimental science. There were experimenters among the
Greeks, notably Ctesibius and Hero, but their work was looked upon by
the Greek scholars as a kind of artisanship rather than as science.
In one of Plato's dialogues, Socrates asks a slave certain
questions about a geometric diagram and has him answer and prove a theorem
in doing so. This was Socrates' method of showing that even an utterly
uneducated man could draw truth from out of himself. Nevertheless, it
took an extremely sophisticated man, Socrates, to ask the questions, and
the slave was by no means uneducated, for merely by having been alive and
perceptive for years,he had learned to make many assumptions by observation
and example, without either himself or (apparently) Socrates being completely
aware of it.
Still as late as 1800, influential philosophers such as
Immanuel Kant held that Euclid's axioms
represented absolute truth.
But do they? Would anyone question the statement that 'the
whole is greater than the part'? Since 10 can be broken up into 6 + 4,
are we not completely right in assuming that 10 is greater than either 6
or 4? If an astronaut can get into a space capsule, would we not be right
in assuming that the volume of the capsule is greater than the volume of
the astronaut?
[Can a TARDIS fit inside a TARDIS? -Will Self]
How could we doubt the general truth of the axiom? Well, any list of consecutive
numbers can be divided into odd numbers and even numbers, so that we might
conclude that in any such list of consecutive numbers, the total of all numbers
present must be greater than the total of even numbers. And yet if we consider
an infinite list of consecutive numbers, it turns out that the total number
of all the numbers is equal to the total number of all the even numbers.
In what is called 'transfinite mathematics' the particular axiom about the
whole being greater than the part simply does not apply.
Again, suppose that two automobiles travel between points A and B by identical
routes. The two routes coincide. Are they equal? Not necessarily. The first
automobile traveled from A to B, while the second traveled from B to A. In
other words, two lines might coincide and yet be unequal since the direction
of one might be different from the direction of the other.
Is this just fancy talk? Can a line be said to have direction? Yes, indeed.
A line with direction is a 'vector' and in 'vector mathematics' the rules
aren't quite the same as in ordinary mathematics and things can coincide
without being equal.
In short, then, axioms are not examples of absolute truth and it is very
likely that there is no such thing as absolute truth at all. The axioms
of Euclid are axioms not because they appear as absolute truth out of some
inner enlightenment but only because they seem to be true in the context
of the real world.
And that is why the geometric theorems derived from Euclid's axioms seem
to correspond with what we call reality. They started with what
we call reality.
It is possible to start with any set of axioms, provided they are not
self-contradictory, and work up a system of theorems consistent with those
axioms and with each other, even though they are not consistent with what
we think of as the real world. This does not make the 'arbitrary mathematics'
less 'true' than the one starting from Euclid's axioms, only less useful,
perhaps. Indeed, an 'arbitrary mathematics' may be more useful than
ordinary 'common-sense' mathematics in special regions such as those of
transfinites or of vectors.
Even so, we must not confuse 'useful' and 'true'. Even if an axiomatic
system is so bizarre as to be useful in no conceivable practical sense, we
can nevertheless say nothing about its 'truth'. If it is self-consistent
that is all we have a right to demand of any system of thought. 'Truth'
and 'reality' are theological words, not scientific ones.
But back to Euclid's axioms. So far I have only listed the five
'common notions'. There were also five more axioms on the list that were
specifically applicable to
geometry and these were later called 'postulates'. The first of these postulates
was:
(1) It is possible to draw a straight line from any point to any other
point.
This seems eminently acceptable, but are you sure? Can you prove that you
can draw a line from the Earth to the Sun? if you could somehow stand on
the Sun safely and hold the Earth motionless in its orbit, and somehow stretch
a string from the Earth to the Sun and pull it absolutely taut, that string
would represent a straight line from Earth to Sun. You're sure that this
is a reasonable 'thought experiment' and I'm sure it is, too, but we only
assume that matters can be so. We can't ever demonstrate them, or prove them
mathematically. And, incidentally, what is
a straight line? I have just made the assumption that if a string is
pulled absolutely taut, it has a shape we would recognize as what we call
a straight line. But what is that shape? We simply can't do better than say,
'A straight line is something very, very thin and very, very straight', or,
to paraphrase Gertrude Stein, 'A straight line is a straight line is a straight
line-'
Euclid defines a straight line as 'a line which lies evenly with the points
on itself,' but I would hate to have to try to describe what he means by
that statement to a student beginning the study of geometry.
Another definition says that: A straight line is the shortest distance between
two points.
But if a string is pulled absolutely taut, it cannot go from the point at
one end to the point at the other in any shorter distance, so that to say
that a straight line is the shortest distance between two points is the same
as saying that it has the shape of an absolutely taut string, and we can
still say 'And what shape is that?'
In modern geometry, straight lines are not defined at all. What is said,
in essence, is this: Let us call something a line which has the following
properties in connection with other undefined terms like 'point', 'plane',
'between', 'continuous', and so on. Then the properties are listed.
Be that as it may, here are the remaining postulates of
Euclid:
(2) A finite straight line can be extended continuously in a straight
line.
(3) A circle can be described with any point as center and any distance as
radius.
(4) All right angles are equal.
(5) If a straight line falling on two straight lines makes the interior angles
on the same side less than two right angles, the two straight lines, if produced
indefinitely, meet on that side on which are the angles less than the two
right angles.
I trust you notice something at once. Of all the ten axioms
of Euclid, only one - the fifth
postulate is a long jaw-breaker of a sentence; and only one -
the fifth postulate - doesn't make instant sense.
Take any intelligent person who has studied arithmetic and who has heard
of straight lines and circles and give him the ten axioms one by one and
let him think a moment and he will say, 'Of course!' to each of the first
nine. Then recite the fifth postulate and he will surely say, 'What!'
And it will take a long time before he understands what's going on. In fact,
I wouldn't undertake to explain it myself without a diagram like the one
below.
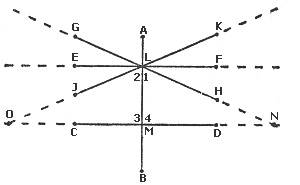 |
Consider two of the solid lines in the diagram: the one that
runs from point C to point D through point M (call it line CD after the end
points) and the one that runs through points G, L, and H (line GH). A third
line, which runs through points A, L, M, and B (line AB), crosses both GH
and CD, making angles with both.
If line CD is supposed to be perfectly horizontal, and line AB is supposed
to be perfectly vertical, then the four angles made in the crossing of the
two lines (angles CMB, BMD, DML, and LMC) are right angles and are all equal
postulate 4). In particular, angles DML and LMC, which I have numbered in
the diagram as 3 and 4, are equal, and are both right angles.
(I haven't bothered to define 'perfectly horizontal' or 'perfectly vertical'
or 'crosses' or to explain why the crossing of a perfectly horizontal line
with a perfectly vertical line produces four right angles, but I am making
no pretense of being completely rigorous. This sort of thing can be
made rigorous but only at the expense of a lot more talk than I am prepared
to give.)
Now consider line GH. It is not perfectly horizontal. That means the angles
it produces at its intersection (I haven't defined 'intersection') with line
AB are not right angles and are not all equal. It can be shown that angles
ALH and GLB are equal and that angles HLB and GLA are equal but that either
of the first pair is not equal to either of the second pair. In particular,
angle GLB (labeled 2) is not equal to angle HLB (labeled 1).
Suppose we draw line EF, passing through L, and that line EF is (like line
CD) perfectly horizontal. In that case it makes four equal right angles at
its intersection with line AB. In particular, angles FLB and ELB are right
angles. But angle HLB is contained within angle FLB (what does 'is contained
within' mean?) with room to spare. Since angle HLB is only part of FLB and
the latter is a right angle then angle HLB (angle 1) is less than a right
angle, by the fifth 'common notion'.
In the same way, by comparing angle ELB, known to be a right angle, with
angle GLB (angle 2), we can show that angle 2 is greater than a right
angle.
The 'interior angles' of the diagram are those on the side of line GH that
faces line CD, and those on the side of line CD that faces line GH. In other
words, they are angles 1, 2, 3, and 4.
The fifth postulate talks about 'the interior angles on the same side,' that
is, 1 and 4 on one side and 2 and 3 on the other. Since we know that 3 and
4 are right angles; that 1 is less than a right angle, and that 2 is more
than a right angle, we can say that the interior angles on one side, 1 and
4, have a sum less than two right angles, while the interior angles on the
other have a sum greater than two right angles. The fifth postulate now states
that if the lines GH and CD are extended, they will intersect on the side
where the interior angles with a sum less than two right angles are located.
And, indeed, if you look at the diagram you will see that if lines GH and
CD are extended on both sides (dotted lines), they will intersect at point
N on the side of interior angles I and 4. On the other side, they just move
farther and farther apart and clearly will never intersect.
On the other hand, if you draw line JK through L, you would reverse the
situation. Angle 2 would be less than a right angle and angle 1 would be
greater than a right angle (where angle 2 is now angle JLB and angle 1 is
now angle KLB). In that case interior angles 2 and 3 would have a sum less
than two right angles and interior angles 1 and 4 would have a sum greater
than two right angles. If lines JK and CD were extended (dotted lines), they
would intersect at point O on the side of interior angles 2 and 3. On the
other side they would merely diverge further and further.
Now that I've explained the fifth postulate at great length (and even then
only at the cost of being very un-rigorous) you might be willing to say,
'Oh yes, of course. Certainly! It's obvious! '
Maybe, but if something is obvious, it shouldn't require hundreds of words
of explanation. I didn't have to belabor any of the other nine axioms, did
I?
Then again, having explained the fifth postulate, have I proved it?
No, I have only interpreted the meaning of the words and then pointed to
the diagram and said, 'And indeed, if you look at the diagram, you will see-'
But that's only one diagram. And it deals with a perfectly vertical line
crossing two lines of which one is perfectly horizontal. And what if none
of the lines are either vertical or horizontal and none of the interior angles
are right angles? The fifth postulate applies to any line crossing any
two lines and I certainly haven't proved that.
I can draw a million diagrams of different types and show that in each specific
case the postulate holds, but that is not enough. I
must show that it holds in every conceivable case, and this can't be
done by diagrams. A diagram can only make the proof clear; the proof itself
must be derived by permissible logic from more basic premises already proved,
or assumed. This I have not done.
Now let's consider the fifth postulate from the standpoint of
moving lines. Suppose line GH is swiveled about L as a pivot in such a way
that it comes closer and closer to coinciding with line EF.(Does a straight
line remain a straight line while it swivels in this fashion? We can only
assume it does.) As line GH swivels toward line EF, the point of
intersection with line CD point N) moves farther and farther to the right.
If you started with line JK and swiveled it so that it would eventually coincide
with line EF, the intersection point O would move off farther and farther
to the left. If you consider the diagram and make a few markings on it (if
you have to) you will see this for yourself.
But consider line EF itself.When GH has finally swiveled so as to coincide
with line EF, we might say that intersection point N has moved off an infinite
distance to the right (whatever we mean by 'infinite distance') and when
line JK coincides with line EF, the intersection point O has moved off an
infinite distance to the left. Therefore, we can say that line EF and line
CD intersect at two points, one an infinite distance to the right
and one an infinite distance to the left.
Or let us look at it another way. Line EF, being perfectly horizontal, intersects
line AB to make four equal right angles. In that case, angles 1, 2, 3, and
4 are all right angles and all equal. Angles 1 and 4 have a
sum equal to two right angles, and so do angles 2 and 3.
But the fifth postulate says the intersection comes on the side where the
two interior angles have a sum less than two right angles. In the case of
lines EF and CD crossed by line AB, neither set of interior angles has a
sum less than two right angles and there can be an intersection on neither
side.
We have now, by two sets of arguments, demonstrated first that lines EF and
CD intersect at two points, each located an infinite distance away, and second
that lines EF and CD do not intersect at all. Have we found a contradiction
and thus shown that there is something wrong with Euclid's set of axioms?
To avoid a contradiction, we can say that having an intersection at an infinite
distance is equivalent to saying there is no intersection. They are different
ways of saying the same thing. To agree that 'saying a' is equal to 'saying
b' in this case is consistent with all the rest of geometry, so we can
get away with it.
Let us now say that two lines, such as EF and CD, which do not intersect
with each other when extended any finite distance, however great,
are 'parallel'.
Clearly, there is only one line passing through L that can be parallel to
line CD, and that is line EF. Any line through L that does not coincide with
line EF is (however slightly) either of the type of line GH or of line JK,
with an interior angle on one side or the other that is less than a right
angle. This argument is sleight of hand, and not rigorous, but it allows
us to see the point and say: Given a straight line, and a point outside that
line, it is possible to draw one and only one straight line through that
point parallel to the given line.
This statement is entirely equivalent to Euclid's fifth postulate. If Euclid's
fifth postulate is removed and this statement put in its place, the entire
structure of Euclidean geometry remains standing without as much as a quiver.
The version of the postulate that refers to parallel lines sounds
clearer and easier to understand than the way Euclid puts it, because
even the beginning student has some notion of what parallel lines look like,
whereas he may not have the foggiest idea of what interior angles are. That
is why it is in this 'parallel' form that you usually see the postulate in
elementary geometry books.
Actually, though, it isn't really simpler and clearer in this form, for as
soon as you try to explain what you mean by 'parallel' you're going to run
into the matter of interior angles. Or, if you try to avoid that, you'll
run into the problem of talking about lines of infinite length, of intersections
at an infinite distance being equivalent to no intersection, and that's even
worse.
But look, just because I didn't prove the fifth postulate doesn't
mean it can't be proven. Perhaps by some line of argument, exceedingly lengthy,
subtle and ingenious, it is possible to prove the fifth postulate by use
of the other four postulates and the five common notions (or by use of some
additional axiom not included in the list which, however, is much simpler
and more 'obvious' than the fifth postulate is).
Alas, no. For two thousand years mathematicians have now and then tried to
prove the fifth postulate from the other axioms simply because that cursed
fifth postulate was so long and so unobvious that it didn't seem possible
that it could be an axiom. Well, they always failed and it seems certain
they must fail. The fifth postulate is just not contained in the other
axioms or in any list of axioms useful in geometry and simpler than itself.
It can be argued, in fact, that the fifth postulate is Euclid's greatest
achievement. By some remarkable leap of insight, he realized that, given
the nine brief and clearly 'obvious' axioms, he could not prove the fifth
postulate and that he could not do without it either, and that, therefore,
long and complicated though the fifth postulate was, he had to include
it among his assumptions.
So for two thousand years the fifth postulate stood there long, ungainly,
puzzling. It was like a flaw in perfection, a standing reproach to a line
of argument otherwise infinitely stately.
It bothered the very devil out of
mathematicians.
And then, in 1733, an Italian priest, Girolamo Saecheri, got the most brilliant
notion concerning the fifth postulate that anyone had had since the time
of Euclid, but wasn't brilliant enough himself to handle it- Let's go into
that in the next chapter.