 |
The Fivefold Way
|
Ivars Peterson
In its simplest form, a tiling problem in mathematics is not unlike the practical task of covering a floor or wall with ceramic tiles. Tiles in the shape of equilateral triangles, squares, or hexagons are particularly easy to work with and do the job nicely (see Figure 7.16). The simplicity and symmetry of the resulting patterns are reasons why researchers interested in cellular automata tend to stick to triangular, square, and hexagonal grids for their models.
An undecorated, triangular tile with sides of equal length has a threefold symmetry. When it is rotated through one-third of a circle,or 120 degrees, nothing seems to change, In its new position , the tile looks just as it did In its old position. That isn't necessarily true of a decorated tile carrying a pattern. Three 120 degree rotations,through a total of 360 degrees, bring the tile back to its original position.
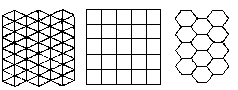
FIGURE 7.16 Regular polygons, such as triangles, squares, and hexagons, can be put together to generate symmetric tilings.
Similarly , plain, square tiles have a fourfold symmetry , and hexagons have a sixfold symmetry.
The same symmetry considerations also apply to the patterns formed when tiles are laid down side by side. If a pattern can be rotated through, say, 90 degrees, and it appears identical to the pattern in its original orientation, then it. too, has a fourfold symmetry.
Tiles in the shape of regular pentagons, with five sides of equal length, have a fivefold symmetry. Attempts to lay such tiles out on a flat surface invariably leave embarrassing gaps in the patterns because the pentagons don't fit together to cover a plane completely.
Using a pair of figures that came to be known as darts and kites, mathematical physicist Roger Penrose of Oxford University solved the pentagon tiling problem in 1974. His discovery came in the course of a search for tile shapes that can tile the plane nonperiodically but not periodically. Whereas a tiling pattern made up of, say, squares repeats itself at regular intervals, and the tiles line up in neat rows that are whole-number distances apart, the resulting pattern in the kite-and-dart case doesn't repeat itself at regular, whole - number intervals. Instead, the irrational number ( 1 + Ö5)/2, also known as the golden ratio or mean, pervades the pattern.
A pair of the required shapes - a dart and a kite - can be created by cutting a rhombus, a figure resembling a skewed square or a diamond, into two pieces in a special way (see Figure 7.17). The rhombus itself must have internal angles of 72 and 108 degrees, Of the two diagonals that can be drawn from corner to corner across the rhombus, the longer one is divided in the golden ratio; that is, one segment ends up roughly 1.618 time. longer than the other. Joining this special point on the diagonal to the other two corners divides the rhombus into two areas.Once piece of the rhombus resembles an arrowhead.
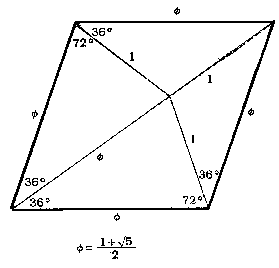
FIGURE 7.17 Dividing a rhombus in a special way produces a kite and a dart.
The other piece. whose blunter end fits snugly into the arrowhead's notch, looks like a diamond with one foreshortened end.
Not surprisingly , when tiling the plane, it's possible to reassemble kites and darts into rhombuses and to arrange these forms in such a way as to create an ordinary, regularly repeating arrangement.To get a nonperiodic pattern, the tiles must be forced to fit together only in certain ways. That can be done by decorating the appropriate sides or angles of each dart and kite with coloured bands or by using small, interlocking tabs like those on jigsaw-puzzle pieces (see Figure 7 18).
Such rules for matching embody the restrictions on how the tiles may be laid down next to one another.
Penrose, working with John Conway, proved there are infinitely many ways to cover the whole plane with kite-and-dart tiles. None of these tilings, or tessellations, is periodic. Some patterns are symmetric, but most are a mystifying blend of apparent order and unexpected deviations. The patterns seem to strive for regularity, but they always fall just short of it.
Although there are an infinite number of possible patterns, one pattern can be distinguished from another only when the tiling, spread out over an infinite plane, is viewed as a whole.An explorer,suddenly parachuted onto such a patterned plane, would have no way of telling on which tiling he had landed. No matter how much he wandered about the plane,he would always find himself in vaguely familiar surroundings,yet he would be forever lost.
Furthermore, in the tightly knit family of Penrose tilings, every finite region in any pattern sits somewhere inside every other pattern. A tourist, wandering across any Penrose tapestry, would eventually encounter, more or less randomly, every possible finite pattern into which the tiles can be formed - a veritable encyclopedia of arrangements.
Remarkably , each plane - filling tiling pattern contains exactly 1.618 . . times as many kites as darts. Because this ratio is an irrational number , it' s impossible to break down the tiling into a single unit cell containing an integral number of each kind of shape.
If it existed, such a unit cell could be used as a building block to construct a periodic Penrose tiling.
To prove that his kite-and-dart tiles really do fill a plane and always produce nonperiodic patterns, Penrose showed that his matching rules are closely related to a set of inflation and deflation rules. Symmetrically bisecting each dart in any tiling, then collecting together the resulting half-darts and kites, makes kites and darts on a larger scale. That is, two half-darts and one kite make a large dart, whereas two half-darts and two kites make a large kite. These larger figures can be used just as easily to build up a complete tiling pattern, and the same process of divide and collect can be applied to them, ad infinitum. The process of inflation guarantees that kites and darts fill the plane (see Figure 7.19).
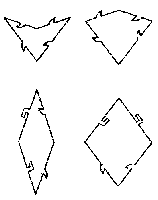
FIGURE 7.18 Adding notches and projections ensures that the tiles can't be put down in a periodic pattern.
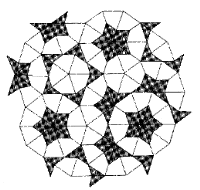
FIGURE 7.19 Inflation rules show that kites and darts fill the plane.
Equivalently, by deflation rules, each tile shape can be divided up into smaller units of the same shape. If each of the tiles in a cluster,constructed according to the matching rules, is divided up or deflated,a new cluster is generated, containing more tiles in which the rules for matching are still obeyed. By repeating the deflation over and over, one can extend the matching rules to a tiling that consists of an infinite number of units. The deflation rule also means that a Penrose tiling' s pattern is self - similar.
As it turns out, there are many different pairs of quadrilateral shapes that form a complete tiling pattern, although all are related in some way to the original kite-and-dart pair. All pairs have characteristic lengths whose ratio is the golden mean. One particularly useful set is a pair of diamond-shaped figures - one fat and one skinny (see Figure 7.20). The skinny diamond has internal angles of 36 and 144 degrees; the fat one, angles of 72 and 108 degrees. Not surprisingly, 1.618 . . . times as many fat diamonds as skinny diamonds are needed for a complete tiling pattern (see Figure 7.2 1 and Colour Plate 16).
Penrose also played the three - dimensional version of his tiling game : packing space with simple blocks, such as pairs of squashed
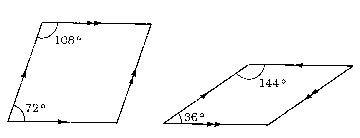
FIGURE 7.20 A pair of rhombuses can also be used to tile a plane.

FIGURE 7.21 A Penrose tiling using thin and fat rhombuses.
cubes (rhombohedra), that generate nonperiodic solid structures with fivefold or, in three dimensions, icosahedral symmetry. The icosahedron, which serves as a model of fivefold symmetry in three dimensions, is a solid figure consisting of 20 identical triangular faces, with 30 edges and 12 vertices. Each vertex lies on one of six fivefold symmetry axes connecting opposite vertices (see Figure 7.22). Just as pentagons can't be used to tile the plane, icosahedra can't be packed together to fill space completely.
Pairs of rhombohedra can, however, be used to fill space, generating the three - dimensional analog of Penrose's kite-and-dart patterns.
Again, no unit cells serve as building blocks, and matching rules lead to nonperiodic structures, where the ratio of the number of rhombohedra of each type is the golden mean.
Penrose tilings have many other intriguing features and suggest a wide range of mathematical questions, many of which haven't been answered yet: Is there a single shape that can tile a plane in a nonperiodic way but cannot tile the plane periodically? Are there pairs of tiles that tile the plane nonperiodically but are not related by the golden ratio?
One perplexing question arises out of the frustrations associated with building a Penrose pattern. It's always possible to continue laying down pieces forever , but finding the right course to take is seldom obvious. Sometimes the choice of where to put a piece is forced, and sometimes there are several alternatives. Making the wrong choice leads to a spot where no piece can legally be put. No one yet knows
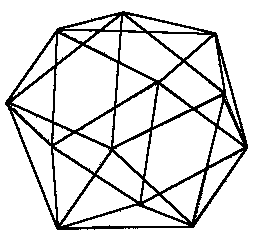
FIGURE 7.22 An icosahedron has a fivefold symmetry in three dimensions.
whether it's theoretically possible to find a general technique for predicting which starting patterns lead to a full tiling of the plane.
Roger Penrose didn't have anything practical in mind for the remarkable tiling patterns he created when he started drawing his diamond tapestries more than a decade ago.The exercise was simply a challenging mathematical game that tickled his fancy.Nevertheless, Penrose did consider some implications of his findings for crystallography, the study of crystal shapes.Although Penrose saw that some concepts crystallographers accepted without question were not always strictly true,he couldn't easily counter the traditional rules that crystallographers had been following for more than a century.
The rules rigidly maintained nonperiodic structures are forbidden because the units of atoms that make up crystals must fall into an orderly,regular arrangement in order to fill space completely.In common salt, for instance, sodium and chloride ions sit at the corners of a cube, and these cubes stack neatly to form each salt crystal.
A few people did take Penrose's ideas seriously,but it took the discovery in 1984 of tiny metallic crystals composed of aluminium and manganese to alert the scientific world to Penrose tilings. These crystals had a form as startling and unexpected as five-pointed snowflakes. X-rays and electrons reflected from the crystals showed Penrose's fivefold symmetry -an event, according to the long standing rules of crystallography, that wasn't possible (see Figure 7.23).
The arrangement of atoms in a solid is comparable to the placement of tiles in a mosaic.
In crystals, atoms or clusters of atoms appear in repeating motifs,analogous to tiles that fill in a mosaic.The repeating motifs,called unit cells, join together to form the complete crystal structure.
Crystal structures generally have a high degree of order.A microscopic observer standing inside a crystal would see row after orderly row of atoms. If the observer were to shift to another position,exactly one unit cell away in any direction.Just as the position of one brick of one brick decides the positions of all the other bricks in a perfectly regular wall, the position of one unit cell determines the positions of all other unit cells.
This requirement for order in a crystal seems to imply that only triangular , square, or hexagonal lattices and variations on these forms have the necessary regularity.According to the well-established suppositions of crystallography,formalized in the branch of mathematics known as group theory [Ref: Davis & Hersh "The Mathematical Experience" {Group Theory}], only a small list of rotational symmetries is possible for crystals.For instance,a crystal is said to have threefold rotational symmetry if the crystal latticework would not change in appearance after the crystal is rotated 120 degrees
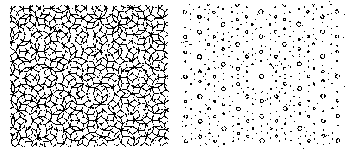
FIGURE 7.23 A Penrose tiling (left) produces a diffraction pattern of spots (right) that has a fivefold symmetry.
about one of its axes. In general, crystals can have twofold, threefold,fourfold, or sixfold axes of rotational symmetry. However, Penrose' s patterns show that fivefold symmetry is possible if more than one unit cell is used and if the need for full geometrical regularity is loosened a bit. In this case, the tiles are neither randomly spaced nor made to fall in neat rows. The position of one tile determines in predictable but subtle ways where the remaining tiles fall. Patterns form, but they never quite repeat themselves, Moreover,each tile of a given shape is oriented along one of a small, discrete set of special directions. For example, Penrose tilings show a scattering of decagons - ten-sided figures that at a distance could be mistaken for circles (see Figure 7.24). All these decagons have the same orientation throughout a pattern : the sides of one decagon are parallel to the corresponding sides of all other decagons.
The newly discovered crystals appear both to be highly ordered and to have a fivefold or, in three dimensions, an icosahedral symmetry. The evidence for both qualities is in the sharply defined spots seen in x-ray and electron diffraction analyses done on the crystals.
The mathematical model that best accounts for these properties seems to be one based on the Penrose tilings. The idea would be to use rhombic triacontrahedra, each of which is made up of ten thin and ten fat rhombohedra, as units to fill space (see Figure 7.25). These units would fit together according to matching rules similar to those that govern Penrose's tilings in two dimensions.
But materials scientists and crystallographers aren't ready to give up their notions of periodicity entirely.They can save the situation to some degree by going into a higher dimension. A simple analogy illustrates the principle involved : suppose a two-dimensional crystal is made up of atoms that sit in a regular square array,a lattice of equidistant points, which is clearly periodic (see Figure 7.26). A line is drawn in a random direction passing through the lattice. If each point in the neighbourhood of the line casts a shadow onto the line,the positions of the shadows will no longer be evenly spaced. Thus an arrangement of points that has neat, evenly spaced rows in
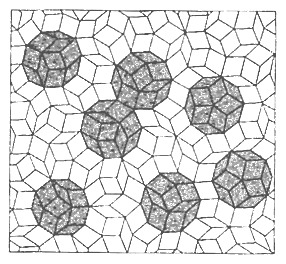
FIGURE 7.24 Decagons have the same orientation throughout the pattern.
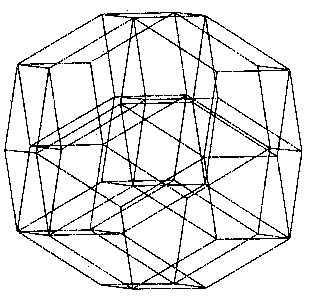
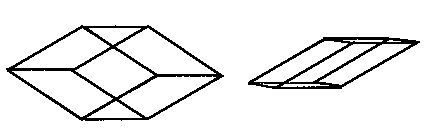
FIGURE 7.25 Sharp and flat rhombohedra can be fitted together to produce a rhombic tricontrahedron.

FIGURE 7.26 A lattice of equidistant points projects onto a quasiperiodic array of points.
two dimensions no longer looks periodic when projected onto a one - dimensional line. In one dimension, the projected points are said to be quasiperiodic.
When a sample of the strange, new crystalline material is rotated in an electron beam, the diffraction patterns show evidence that these crystals have many fivefold as well as twofold and threefold axes. By noting the angles between pairs of these axes, it's possible to conclude that the material has the same symmetry as an icosahedron. The six icosahedral axes showing a fivefold symmetry form the basis for a six-dimensional space. In this space, the crystal would have a cubic unit cell, which means that these unit cells will stack evenly to form a regular, periodic crystal lattice. However, when the six-dimensional structure is viewed as a projection into three dimensions, the periodicity disappears. The three-dimensional projection looks quasiperiodic.
Because the new structures are highly ordered -just like normal crystals - but are quasiperiodic instead of periodic, they came to be called quasiperiodic crystals, or quasicrystals for short, Like Superman, they have a double identity. In six - dimensional space, they lead a regular, perfectly ordinary existence. In three-dimensional space, they have extraordinary properties, breaking the rules that appear to govern other crystalline materials. These new substances bring crystallography into higher dimensions and present crystallographers with a new mathematics to learn.
Of course, the full story isn't quite so simple. Some scientists still dispute the discovery of quasicrystals, claiming that the crystal samples are really made up of twins, which by themselves are regular, but together create the anomalous diffraction patterns. On the other hand, those who accept quasicrystals debate how the atoms within the rhombohedral unit cells may be arranged. They argue the fine points of decoration - the position of each aluminium and manganese atom within the postulated unit cells.
Furthermore, there are ways to describe a quasicrystalline lattice without having to venture into six dimensions. Mathematician Branko Grunbaum, an expert on the mathematics of tilings, argues strongly in favour of adjacencies to describe tilings and crystal forms,an alternative to the group-theory approach traditionally used by crystallographers and other researchers. Whereas group theory emphasizes the importance of a pattern' s overall rotational - symmetry properties, the adjacencies model takes a local approach, specifying how one piece is connected to its neighbours. In fact, adjacency rules generate many interesting patterns that can't be described by symmetries and group theory.
In a sense, the adjacencies way of looking at tilings isn't particularly new. For millennia, artists and craftsmen have created intricate,pleasing designs and repeating patterns on walls, in woven fabrics,on pottery without relying on the tenets of group theory to guide their work. They counted on their own empirical rules and schemes, which more often than not simply stated how one tile or shape fits with another. Once the rules and tile shapes are selected, the types of patterns that emerge are set.
Mathematicians face other challenges as well. They already know that simple matching and inflation rules for various types of two-dimensional tiles can force the creation of patterns not just with a fivefold symmetry but also with eightfold and twelvefold symmetries.
Are there other possibilities? The same question applies to three - dimensional shapes for filling space. Is the icosahedral form the only one that occurs in three dimensions? Even physicists, now on the lookout for even stranger crystalline forms, may be interested in the answers.
And, what happens if the game of ''Life'' is played on a Penrose tiling? How should the rules be modified to keep the game interesting? The prospects are mind boggling.

Plate 16
