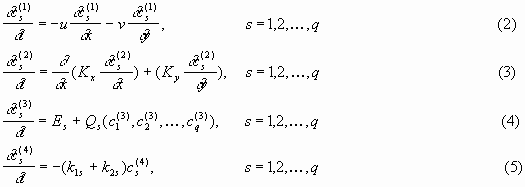|
| |
-
Volume 1
# 1-504-BG; Cod. 504 - Sciences for
environmental
TWO DIMENSIONAL COMPUTER MODELLING
OF LONG RANGE TRANSPORT OF AIR POLLUTANTS
Krassimir T. Georgiev
- Central Laboratory for Parallel Processing
- Bulgarian Academy of Sciences
- 25-A Acad. G. Bonchev str., 1113 Sofia, Bulgaria
Received 10.05.2000; Cited 15.05.2000
Abstract
The task for finding reliable and robust
control strategies for keeping the air pollution under certain safe levels and using these
strategies in a routine way is one of the most important tasks which must be solved in the
modern society. The transboundary transport of air pollutants and the chemical
transformations under the transport (including here the photochemical reactions) are
causing greater and grater problems. It is very important to predict episodes when the
critical levels will be exceeded. This is especially true for summer ozone episodes. Large
mathematical models, in which all physical and chemical processes are adequately
described, in cooperation with the modern high-performance supercomputers can successfully
be used to solve this task. One such a model is the Danish Eulerian Model developed in the
National Environmental Research Institute in Roskilde, Denmark. This model and the new
algorithms for an effective operational run of this model on vector and parallel
supercomputers will be discussed in this paper. Developed codes are portable for parallel
computers with shared and distributed memory, symmetric multiprocessor computers and
clusters of workstations.
Key words: air pollution modelling,
vector and parallel supercomputers, numerical mathematics, algorithms
Subject classifications: 65M20, 65N40,
65N55, 86A35
1. INTRODUCTION
The protection of our environment is one of
the most important problems in the society. The environment protection will become even
more important in the next century. More and more important physical and chemical
mechanisms are to be added to the models (as, for example, mechanisms for describing the
production and transport of fine and ultra fine particles, mechanisms for describing
better the natural emissions, etc.). Moreover, new reliable and robust control strategies
for keeping the pollution caused by harmful chemical compounds under certain safe levels
have to be developed and used in a routine way. The large mathematical models, in which
all physical and chemical processes are adequately described, can successfully be used to
solve this task. The use of such models leads to the treatment of huge computational
tasks. In a typical simulation several thousand time steps have to be carried out and at
each time step systems of ordinary differential equations consist of up to several million
equations have to be solved. The effective solution of such huge tasks require combined
research from specialists from the fields of environmental modelling, numerical analysis
and scientific computing.
The pollution levels in some part of Europe
are so high that preventive action are urgently needed because some damaging effects may
soon become irreversible. The reduction of the emissions is an expensive process and
therefore the solution of the problem for finding robust and reliable control strategies
must be optimal or at least close to the optimal. This is possible only by carrying out
long simulation experiments of many hundreds runs of comprenhesive mathematical models.
Comparing after that the results obtained from different models the answer of the
following important questions can be found: (a) are there any discrepancies and (b) what
are the reasons for these discrepancies. The process of finding the optimal solution is in
general a long process and therefore the efficiency of the computer codes is highly
desirable. Some more computations in real time will be needed in connection with the EU
Ozone directive. High ozone concentrations occur in large parts in Europe during the
summer season and they can cause damages. Reliable mathematical models have to be coupled
with weather forecasting models and they have to be run operationally after that in order
to predict the appearance of high concentrations and to help the decision makers in such
situations. The remainder of the paper is organized as follows. Short description of the
mathematical model and the splitting procedure used one can find in Section 2. Section 3
focuses on the numerical techniques, computer treatment and some numerical results
obtained while real data set was used. The final Section 4 summarizes our conclusions and
outlook.
2. MATHEMATICAL MODEL AND
SPLITTING
The physical phenomenon, which is well
known under the name Long Range Transport of Air Pollution (LRTAP) consists of three major
stages:
- Emission. Different pollutants are emitted in the atmosphere
from different emission sources. Many of them are anthropogenic but some of the pollutants
are emitted also from natural emission sources.
- Transport. The actual transport of the pollutants is due to
the wind. This is normally called advection of the air pollutants.
- Transformations during the transport. Three major processes
take place:
- Diffusion. The air pollutants are widely
dispersed in the atmosphere.
- Deposition. Some of the pollutants are
deposited to the surface of the Earth (soil, water and vegetation). Two different kind of
deposition is considered: dry deposition (continues throughout the long-range transport)
and wet deposition (takes place only when it rains)
- Chemical reactions. Due to some chemical
reactions many secondary pollutants are created.
Mathematically, the air pollution
phenomenon, can be described by the so called Eulerian approach where the behavior of the
species is described relative to a fixed coordinate system or by so called Lagrangian
approach where the changes of the concentrations are described relative to the moving
fluid. The Eulerian approach will be used in this paper because the Eulerian statistics
are readily measurable and the mathematical expressions are directly applicable to
situations in which the chemical reactions take place [9]. Hereafter we will pay attention
on the Danish Eulerian Model for Long-range transport of Air Pollutants developed at the
Danish National Environmental Institute in Roskilde [12, 13, 14].
Let us denote the number of the pollutants
under consideration with q. Let W be a bounded domain with boundary G= W. The following system of partial differential equations is an
adequately mathematical description of the Eulerian model for the long-range transport of
air pollutants [11]. W. The following system of partial differential equations is an
adequately mathematical description of the Eulerian model for the long-range transport of
air pollutants [11].
  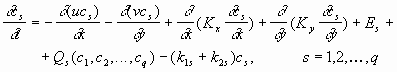 (1) (1)
where 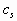 are the
concentrations; are the
concentrations; 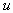 and and 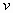 are the wind
velocities; are the wind
velocities; 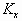 and and 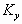 are the diffusion
coefficients; the sources are described by are the diffusion
coefficients; the sources are described by 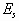 , ,
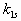 and and 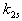 are the deposition coefficients and
the chemical reactions are represented by function are the deposition coefficients and
the chemical reactions are represented by function 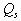 . Often
advection part of the equations which is described by the first two terms in the
right-hand side of (1) can be simplified by assuming that a conservation low is satisfied
in the lower part of the atmosphere, and we will use this assumption in our model. The
chemical processes presented by . Often
advection part of the equations which is described by the first two terms in the
right-hand side of (1) can be simplified by assuming that a conservation low is satisfied
in the lower part of the atmosphere, and we will use this assumption in our model. The
chemical processes presented by 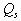 , play a special role in the
model. The equations in the system (1) is coupled only through the chemical reactions.
From the other hand, the chemistry introduced nonlinearity in the model. The chemical
reactions are of the form: , play a special role in the
model. The equations in the system (1) is coupled only through the chemical reactions.
From the other hand, the chemistry introduced nonlinearity in the model. The chemical
reactions are of the form:
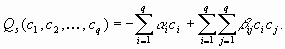
Initial and boundary conditions are added
to the system of partial differential equations (1).
It is very difficult to treat numerically
the system (1). One way to find an efficient solution of this problem is to apply some
splitting procedure. Following the ideas in Marchuk [7] and McRae et al [8] the model is
divided in four submodels according to the different processes which are involved in:
advection, diffusion, deposition and chemistry (together with source term) as follows:
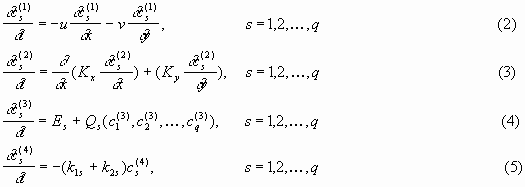
These submodels are discretized using
different discretisation algorithms and treated successively at each time-step (see for
example [1, 2, 3, 10, 11, 15]). The initial conditions are used to couple the four systems
(2) - (5). Consider a given time step  ).
The initial conditions used in the solution of (2) is a vector containing the
concentrations at the grid-points which were obtained during the previous time step, i.e.
the time step ( ).
The initial conditions used in the solution of (2) is a vector containing the
concentrations at the grid-points which were obtained during the previous time step, i.e.
the time step (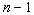 ). The approximation
obtained after the solution of (2) is used as initial conditions for (3), etc. The
approximate solution obtained after the solution of the fourth system (5) is considered as
an acceptable approximation of the concentrations at step n and the procedure continues
with the next time step. ). The approximation
obtained after the solution of (2) is used as initial conditions for (3), etc. The
approximate solution obtained after the solution of the fourth system (5) is considered as
an acceptable approximation of the concentrations at step n and the procedure continues
with the next time step.
3. COMPUTER TREATMENT AND NUMERICAL
RESULTS
The space domain into the operational two
dimensional version of the Danish Eulerian Model contains all of Europe, parts of Asia,
Africa and the Atlantic Ocean. It is a square with side of 4800 km. In the last few years
the most often use space discretization is on (96 x 96) grid which means small squares
with side of 50 km while the number of air pollutants studied is 35, i.e. 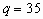 in (1) - (5). This leads to the treatment of
four systems of ordinary differential equations per time-step and each of them contains
322 560 equations. It is desirable to implement chemical schemes containing more species
(chemical schemes with 56 and 168 species have been extensively tested but these schemes
are still not used for operational purposes). Very often more detailed output information
is needed. A better resolution of 10 km leads to space discretization on (480 x 480) grid.
Then each of the four systems of ordinary differential equations described above will
consist of 8 064 000 equations in this two dimensional case. This very short description
of the numerical difficulties which arise when large air pollution models are to be
treated explains why the search for more efficient numerical methods and algorithms is
continuing. Moreover, the more often time-period for one run of the model is one month
which requires 3456 time-steps when the time step for the advection part is 900 sec. Let
us note that the systems of ordinary differential equations in the chemical part are stiff
and therefore they have to be treated with smaller time-steps (150 sec is used in the
model under consideration) [11]. It is clear that the computational task has to be solved
is enormous and it causes great difficulties even when big and fast modern supercomputers
are used. Therefore it is essential to select both sufficiently accurate and fast
algorithms and optimize the code for runs on parallel computers (with shared and
distributed memory, including here the clusters of workstations) and vector computers. The
parallel version of the Danish Eulerian Model which is actually used on parallel computers
is based on the partitioning of the computational domain in several subdomains, The number
of these subdomains are equal to the number of the processors which are available. As was
mentioned above different numerical algorithms are used in the different submodels. The
major numerical method used in the advection/diffusion part is linear finite element
method while the quasi study state approximation (QSSA) algorithm is used the chemical
part [5]. More about the numerical methods and algorithms used in the Danish Eulerian
Model one can find in[11]. Therefore, two types of subdomains are appeared -
nonoverlapping for the chemical and deposition parts and overlapping for the advection and
diffusion parts. in (1) - (5). This leads to the treatment of
four systems of ordinary differential equations per time-step and each of them contains
322 560 equations. It is desirable to implement chemical schemes containing more species
(chemical schemes with 56 and 168 species have been extensively tested but these schemes
are still not used for operational purposes). Very often more detailed output information
is needed. A better resolution of 10 km leads to space discretization on (480 x 480) grid.
Then each of the four systems of ordinary differential equations described above will
consist of 8 064 000 equations in this two dimensional case. This very short description
of the numerical difficulties which arise when large air pollution models are to be
treated explains why the search for more efficient numerical methods and algorithms is
continuing. Moreover, the more often time-period for one run of the model is one month
which requires 3456 time-steps when the time step for the advection part is 900 sec. Let
us note that the systems of ordinary differential equations in the chemical part are stiff
and therefore they have to be treated with smaller time-steps (150 sec is used in the
model under consideration) [11]. It is clear that the computational task has to be solved
is enormous and it causes great difficulties even when big and fast modern supercomputers
are used. Therefore it is essential to select both sufficiently accurate and fast
algorithms and optimize the code for runs on parallel computers (with shared and
distributed memory, including here the clusters of workstations) and vector computers. The
parallel version of the Danish Eulerian Model which is actually used on parallel computers
is based on the partitioning of the computational domain in several subdomains, The number
of these subdomains are equal to the number of the processors which are available. As was
mentioned above different numerical algorithms are used in the different submodels. The
major numerical method used in the advection/diffusion part is linear finite element
method while the quasi study state approximation (QSSA) algorithm is used the chemical
part [5]. More about the numerical methods and algorithms used in the Danish Eulerian
Model one can find in[11]. Therefore, two types of subdomains are appeared -
nonoverlapping for the chemical and deposition parts and overlapping for the advection and
diffusion parts.
The input data for the Danish Eulerian
Model may be divided as emission and meteorological input data. The input data are
organized in different files and consist: ammonia, sulphur, nitrogen and antropogenic VOC
emissions. An information about the forests is used to prepare the natural VOC emissions
by the algorithm of Lubkert and Shop [6]. There is an input file with latitudes and
longitudes of the grid points. The meteorological data are organized in eight files and
consist information about cloud covers, humidity, mixing height, precipitation,
temperature, surface temperature, vertical and horizontal components of the wind velocity.
The total amount of the input data for the most often used time interval of one month are
more than 54 Mbytes. All these data are obtained from the Norwegian Meteorological
Institute. The data are for all grid points and for every 6 or 12 hours during the time
interval. The output data for the same time interval is even more. Experiments with
different emission scenarios resulted in collecting very large output data set. The total
amount of these data is greater than 100 Mbytes (see e.g. [1]). These data include the
meanvalues of the: concentrations per month, per day and per hour, concentrations in
precipitations per month and per day and depositions per month.
The numerical results reported in this
paper were performed on the vector computer CRAY C92A with top performance 0.9 GFlops
(billions of floating point computations per second) (see Table 1) and the parallel
computer IBM SP Power 2 with up to 32 120 MHz RS/6000 processors, each of them with top
performance 0.48 GFlops (see Tables 2 and 3). The speedup (Sp) is defined as the computing
time on p processors divided by the computing time two processors (in Table 2) and one
processor (in Table 1). The parallel efficiency is defined as Ep=Sp/p while the
computational efficiency as 100*GFlops/(p*top-performance).
Table 1. Results
obtained on CRAY C92A computer.
Computing
time (in sec) |
1360 |
Computational
speed (in GFlops) |
0.446 |
| Computational
efficiency (in percent) |
49.5 |
Table 2. Results obtained
on IBM SP Power 2 computer.
Number of
processors |
1 |
2 |
4 |
8 |
16 |
32 |
Computing time
(in sec) |
20154 |
3875 |
1784 |
921 |
464 |
258 |
Speedup (Sp) |
- |
- |
2.17 |
4.21 |
8.35 |
15.02 |
Parallel
efficiency (Ep) |
- |
- |
1.09 |
1.05 |
1.04 |
0.94 |
Comput. speed
(in GFlops) |
0.03 |
0.156 |
0.339 |
0.657 |
1.304 |
2.35 |
Comput.
efficiency (Cp) |
6% |
16% |
18% |
17% |
17% |
15% |
The parallel algorithm leads to a
considerable reduction of the computational times and it is well seen from Table 1 and
Table 2 that the best computing time obtained on IBM SP computer platform is are more than
five times better than the computing time obtained on CRAY computer. However, the
efficiency of the vector variant of the algorithm is much better than the efficiency of
the parallel variant of the algorithm. The superlinear speedups which can be seen in some
of the runs (see Table 2) can be explained with the increasing memory locality, the cache
locality and the communication overhead. The main problems with cache locality are in the
chemical submodel. The improvement of the algorithm in this part was done by using so
called chunks, i.e. computations in the chemical part to be done in small portions. The
size of the chunks depends on the size of the cache memory of the processors used. This
allows to use in better way the cache memory of the processors. This approach has an
additional advantage because it leads to considerable savings of storage (for more details
see [2, 3, 4]).
Table 3. Results
obtained on IBM SP Power 2 computer with effective use of the cache memory
Number of
processors |
1 |
2 |
Computing time
(in sec) |
7017 |
3529 |
Speedup (Sp) |
- |
1.99 |
Parallel
efficiency (Ep) |
- |
0.99 |
Comput. speed (in
GFlops) |
0.09 |
0.172 |
Comput.
efficiency (Cp) |
18% |
18% |
Comparing the results given in the first
two columns of Table 2 and Table 3 one can see that even for one processor we obtained a
reasonable computing time (decreased with 63% for one processor and with 9% for two
processors. Furthermore, there is no superlinear speedup, there is an excellent parallel
efficiency and the computational efficiency was improved with 12% in the case of one
processor run and with 2% when two processors were used.
4. CONCLUDING REAMARKS
The modern environmental studies indicate
that the complex and advanced air pollution models are needed. Many pollutants have to be
included and advanced chemical modules with nonlinear chemical reactions are to be
attached to such models. New and more reliable physical parametrizations have to be
chosen. This will reflect in very big models and the treatment of such models will be very
time consuming even when high-performance computers are used. Therefore, the work of
finding efficient numerical methods and algorithms for their realization on vector and
parallel computers has to continue. The codes should be adjusted to the particular
computer which is available. The use of standard message passing interface (MPI), which is
practically used in our code, is a key component in the development of concurent computing
environment in which applications and tools can be transparently ported between different
computer platforms. From our experiments it is seen that there is a big gap between the
top performance of the computers and the performance which is really achieved. Our
experience show that the partitioning of the computational domain in several subdomains
and use parallel computers for runs of the model allows to solve efficiently the
large-scale problems in air pollution modelling. The parallel version of the Danish
Eulerian model is a good tool because I leads to a considerable reduction of the
computational time as well as to possibility to store different parts of the input and
output data, and different parts of the coefficient matrices which are appeared after the
space discretization procedure, into the local memories of the different processors.
Hence, we are able to solve huge real-life problems when the problem does not fit in the
memory of a single processor. Due to the short of place we did not stop on the
visualization and animation techniques which are needed in order to present the output
results in more understandable way. The large air pollution models for long-range
transport of air pollutants create a huge sets of output data, many million of numbers,
and some visualization and/or animation tools have to be used for clearly seeing the
relationships that are expressed by the enormous amount of digital data. Experiments
performed with the Danish Eulerian model have been already used to establish the
dependence between decreasing the emissions in given subdomain or in the whole
computational domain and the behavior of the concentrations (see e.g. [1]) using some
visualization tools. They indicate that for some pollutants the effects are close to
linear (sulphur, ozone, etc.) but for some others the effects are non-linear (nitrogen,
hydroxil radical, etc.) but there are still many open questions and it is necessary to
perform many a lot of systematic computations in order to answer these, important for the
society, questions.
ACKNOWLEDGEMENTS
This research was partly supported by the
Ministry of Education and Science of Bulgaria under Grants I-811/98 and I-901/99.
Furthermore, a grant from the Danish Natural Science Research Council gave us an access to
all Danish supercomputers.
REFERENCES
- Dimov, I., Georgiev, K., Zlatev, Z.: Long-range transport of
air pollutants and source receptor relations, Notes on Numerical Fluid Mechanics, 62
(1998), 155-166
- Georgiev, K., Zlatev, Z.: Application of parallel algorithms
in an air pollution model, NATO Science Series, 2. Environmental Security, Vol. 57 (1999),
173-184
- Georgiev, K., Zlatev, Z.: Parallel sparse matrix algorithms
for air pollution models, Parallel and Distributed Computing Practices (to appear in 2000)
- Georgiev, K., Zlatev, Z.: Some numerical experiments with
the parallel version of the two-dimensional Danish Eulerian model, Notes on Numerical
Fluid Mechanics, 73 (2000), 283-291
- Hesstvedt, E, Hov, O., Isaksen, I: Quasi-steady-state
approximations in air pollution modelling: comparison of two numerical schemes for oxident
prediction, Int. J. of Chemical Kinetics, 10 (1978), 971-994
- Lubkert, B., Schopp, W.: A model to calculate natural VOC
emissions from forests in Europe, Report No. WP-89-082, IIASA, Laxenburg, Austria (1989)
- Marchuk, G., Mathematical modelling for the problem of
environment, Studies in Mathematics and Applications, 16 (1985), North-Holland, Amsterdam
- McRae, C., Goodin, W., Seinfeld, J.: Numerical solution of
the atmospheric diffusion equations for chemically reacting flows, J. of computational
Physics, 45 (1984), 1-42
- Seinfeld, J.: Air Pollution, Wiley, New York (1986)
- Zlatev, Z..: Application of predictor-corrector
schemes with several correctors in solving air pollution problems, BIT, 24 (1984), 700-715
- Zlatev, Z..: Computer treatment of large air pollution
models, Kluwer Academic Publ., Dordrecht-Boston-London (1995)
- Zlatev, Z.., Christensen, J., Eliassen, A.: Studying high
ozone concentrations by using the Danish Eulerian model, Atmospheric Environment, 27A
(1993), 845-865
- Zlatev, Z.., Christensen, J., Hov, O.: An Eulerian air
pollution model for Europe with nonlinear chemistry, J. of Atmospheric Chemistry, 15
(1992), 1-37
- Zlatev, Z.., Dimov, I., Georgiev, K.: Three-dimensional
version of the Danish Eulerian model, ZAMM, 76 (1996), 473-476
- Zlatev, Z.., Dimov, I., Georgiev, K.: Modelling the
long-range transport of air pollutants, IEEE
Computational Science & Engineering, 1 (3) (1994), 45-52
|


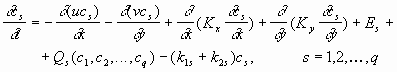 (1)
(1)