Eletrônica Digital - Representação de Números com Sinal

Aritmética

Representação de Números com Sinal

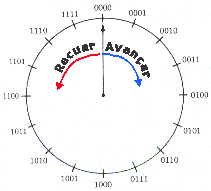
A representação de números em registradores usa os estados SET e RESET dos flip-flops para representar os numerais 0 e 1, respectivamente.Caso se use um registrador de 4-bits, o registrador teria dezesseis posições(estados) e pode registrar os números de 0 a 15. A representação da figura abaixo está em forma circular para lembrar que o registrador tem um número finito de estados e após passar por cada estado, volta para o estado inicial e retoma o ciclo novamente.O registrador pode ser designado como um registrado de módulo 16(2ⁿ) , onde n é o número de bits do contador, ou um registrador de módulo de quatro de casas.

		Este modo de representar o registrador indica que o ponteiro, que representa a propriedade do registrador de 'girar' pelos seus estados em resposta ao pulso de relógio, pode ser usado para efetuar operações aritméticas. Operação Contar: avançar ou recuar o ponteiro uma posição para indicar uma contagem adicional. Operação Somar: Limpar o registrador(resetar, o ponteiro aponta para 0000); avançar o ponteiro para a posição da primeira parcela e, em seguida, avançar o ponteiro um número de estados igual à segunda parcela; a posição final do ponteiro indicará o resultado da operação. Operação Subtrair: Limpar o registrador(ponteiro em 0000); em seguida, o

	Fig.1
ponteiro é deslocado para a posição da primeira parcela(minuendo); depois o ponteiro deve recuar o número de posições igual ao valor da segunda parcela(subtraendo).Assim, o ponteiro indicará a posição igual ao valor da subtração.Observe que as operações são válidas somente dentro do módulo do registrados, isto é, operações no intervalo de 0 a 15.

Representação de Números por Sinal-Magnitude

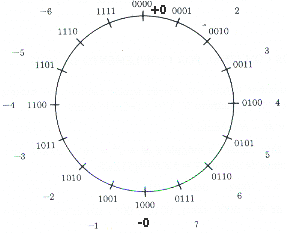
Para representar números com sinal, se usa o flip-flop da posição mais significativa(MSB) do registrador para indicar o sinal do número. A convenção adotada é que se o bit de sinal é igual a 0, o número é positivo; se o bit de sinal é igual a 1, então o número é negativo.A Fig.2 mostra o registrador módulo 16 com números positivos e negativos.Observe que existem, na representação sinal-magnitude dois 0, -0=1000 e +0=0000. A existência de dois 0 torna a representação sinal-magnitude díficil de ser usada para operações no registrador simplesmente avançando ou recuando o ponteiro.A Fig.3 tem um exemplo para o número 52, representado com 7 bits, 6 bits para magnitude e 1 bit, o MSB, de sinal.



					Fig.3
		Fig.2

Representação de Números com Sinal em Complemento-de-Dois
O complemento-de-dois de um número N qualquer, no módulo M, é definido como o módulo M menos o número N e representado por N⁽²⁾.

N⁽²⁾=M-N

Observe que o valor do complemento-de-dois de um número depende do módulo do registrador, isto é, de quantos bits são usados para escrever o número.Então, o mesmo número tem complemento-de-dois diferentes se está em um registrador de 4-bits(M=16) ou em registrador de 5-bits(M=32).

Se N=0101, o módulo M=16₁₀=10000, então N⁽²⁾=10000-0101=1011.

Caso o módulo seja M=32₁₀=100000, então N⁽²⁾=100000-00101=11011.

O complemento-de-dois de número não pode ser especificado com certeza a não ser que o módulo seja especificado.A avaliação do complemento-de-dois de um número envolve uma sucessão de subtrações, bit a bit, do número binário 10(2₁₀).

Algoritmo para obter o complemento-de-dois de um número

Escrever o número com tantos bits quantos forem os do registrador onde armazenado o número.

Começando com o bit menos significativo, percorrer o número da direita para esquerda, deixando inalterados os bits iguais a 0 até encontrar o primeiro 1, deixar este 1 inalterado.

Complementar os demais bits do número.

Assim, o sistema de representação por complemento-de-dois de números com sinal estabelece que o negativo de um número qualquer N é dado pelo complemento-de-dois do número N. Então, dado N qualquer,

-N=N⁽²)=M-N

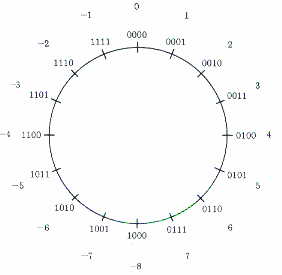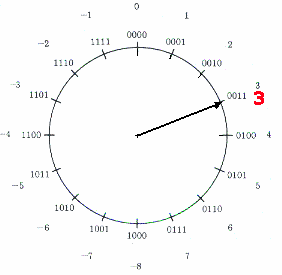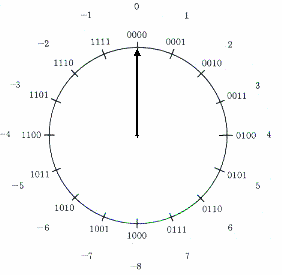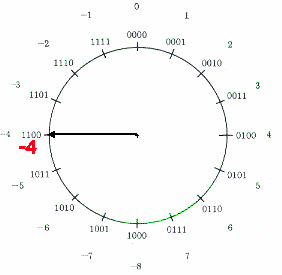
O registrador de módulo de quatro casas tem apenas um único 0 e fornecerá os números no intervalo -8 até +7, como mostra a Fig.4. O bit mais a esquerda(MSB) indica o sinal do número: se fôr igual a 0, o número é positivo; se o MSB é igual a 1, o número é negativo(na representação complemento-de-dois). A representação por complemento-de-dois, permite que a soma seja feita pelo avanço e a subtração pelo retardo do ponteiro.O resultado da operação deve se encontrar dentro do intervalo do registrador.

			Por exemplo, seja a operação 3-7 a ser realizada no registrador de quatro casas da Fig.4. ajustar o ponteiro em 0000 para resetar o registrador avançar três posições e o ponteiro indica o minuendo 3(0011) recuar sete posições ( valor do subtraendo 7) o ponteiro indicará 1100 que é igual a -4 na representação em complemento-de-dois
	Fig.4

A representação de números binários em complemento-de-dois torna possível transformar a operação de subtração em uma operação de soma, eliminando o problema de recuar o ponteiro do registrador.

Sejam N1 e N2 números binários quaisquer, então,

N₁-N₂=N₁+(-N₂)=N₁+N₂⁽²⁾

Assim, a subtração de dois números binários pode ser obtida fazendo a soma do minuendo com o complemento-de-dois do subtraendo.Agora, o registrador sempre realizará operações de soma, avançando o ponteiro, e o mesmo circuito efetua adição e subtração.

Representação de Números com Sinal em Complemento-de-Um

O complemento-de-um de N, número binário qualquer, no módulo M, é dado por

N⁽¹⁾=(M-1)-N

onde M=2ⁿ, sendo n o número de bits do registrador.

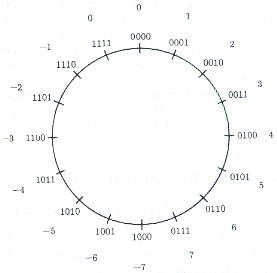			A Fig.5 mostra a representação em complemento-de-um para um registrador de quatro casas. Veja que existem dois 0s(zeros): 0000 e 1111. Os circuitos são mais complicados para projetar. Se N=0101, o módulo M=16₁₀=10000, então N⁽¹⁾=(10000-1)-0101=1111-0101=1010. Caso o módulo seja M=32₁₀=100000, então N⁽¹⁾=(100000-1)-00101=11111-00101=11010. A determinação do complemento-de-um de um número é obtida através de sucessivas subtrações, dígito a dígito, do número 1.O complemento-de-um pode ser calculado complementando bit a bit o número original, como mostra os exemplos acima.
	Fig.5

Usando a representação por complemento-de-um pode-se obter o complemento-de-dois de um número adicionando 1 ao complemento-de-um.

N⁽²⁾=M-N e N⁽¹⁾=(M-1)-N, então N⁽¹⁾=(M-N)-1=N⁽²⁾-1 , assim N⁽¹⁾=N⁽²⁾-1

N⁽²⁾=N⁽¹⁾+1

Para se obter o complemento-de-dois de um número binário deve-se escrever o número com a quantidade de bits do registrador, complementar o número bit a bit e somar 1 ao resultado.