

Soma de Números Binários
Sejam A e B números binários de n dígitos cada e S, a soma de A mais B, um número binário de n+1 dígitos, então o dígito Si é determinado unicamente pelos dígitos Ai e Bi de A e B.
Circuito Meio-Somador
Os métodos de soma de números binários envolvem a soma de dígitos coluna a coluna.Então, a adição de dois números binários Ai e Bi pode ser calculada conforme mostrado abaixo.
 |
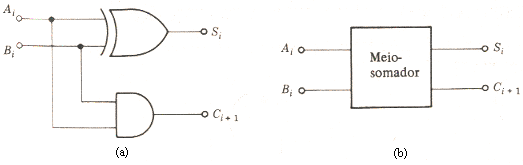
A Fig.1(a) mostra as adições de dois dígitos binários . A soma gera um dígito soma Si na mesma i-ésima coluna que tem a mesma significância númerica que Ai e Bi. A soma pode gerar um dígito de vai-um Ci+1 que tem significância numérica maior que as parcelas Ai e Bi. A Fig.1(b) mostra a tabela verdade para as somas feitas na Fig.1(a); uma linha para cada operação e as saídas Si e Ci+1. |
|||
| Fig.1 | ||||
Os circuitos para realizar as somas acima e fornecer as saídas Si e Ci+1 podem ser derivados da tabela verdade da Fig.1(b). A parcela soma Si pode ser obtida pelo XOR de Ai e Bi. O dígito vai-um Ci+1 é dado por um AND de Ai e Bi. A Fig.2(a) mostra o circuito lógico de portas e a Fig.2(b) o símbolo. A estrutura que soma dois dígitos binários é designada como Meio-Somador, e abreviada como HA(Half Adder).
Circuito Somador Inteiro
A soma coluna por coluna de dois números binários de n dígitos produz um vai-um Ci+1 que deve ser somado na próxima coluna de maior significância.
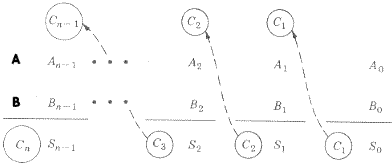
Fig.3
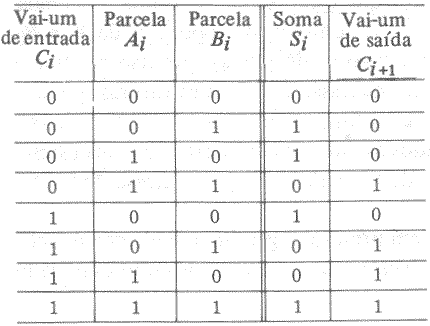
O meio-somador só pode realizar a primeira operação de A0 mais B0; nas outras colunas são necessárias a adição de três bits Ai, Bi e Ci(vai-um da coluna i-1).O dígito mais significativo da soma é o dígito vai-um para coluna n, ou seja Cn.Assim, na soma de Ai, Bi e o vai-um Ci são gerados Si e o vai-um Ci+1.A tabela verdade abaixo mostra a geração dos bits soma Si e vai-um Ci+1.
O meio-somador só pode realizar a primeira operação de A0 mais B0; nas outras colunas são necessárias a adição de três bits Ai, Bi e Ci(vai-um da coluna i-1).O dígito mais significativo da soma é o dígito vai-um para coluna n, ou seja Cn.Assim, na soma de Ai, Bi e o vai-um Ci são gerados Si e o vai-um Ci+1. A tabela verdade da Fig.4 mostra a geração dos bits soma Si e vai-um Ci+1. |
 |
||||
| Fig.4 | |||||
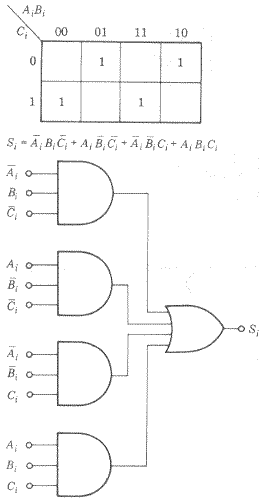
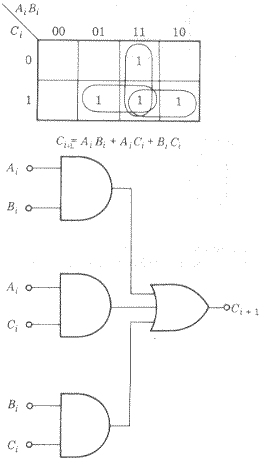
Os circuitos lógicos para geraçao do bit soma Si e do bit de vai-um Ci+1 podem ser obtidos diretamente dos mapas K para cada saída da tabela verdade da Fig.4.
| Soma Si | Vai-Um Ci+1 | ||||||||
 |
|||||||||
 |
|||||||||
| Fig.6 | |||||||||
| Fig.5 | |||||||||
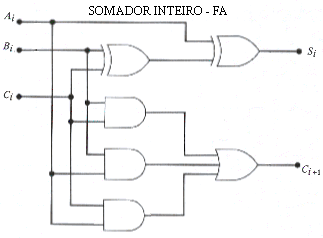
Através de simplificações algébricas pode-se mostrar que o bit soma Si é igual ao XOR das entradas Ai, Bi, e Ci.Então, o circuito de portas lógicas para soma três bits chama-se Somador Inteiro( Full Adder), designada FA, e tem a estrutura e símbolos mostrados abaixo.
 |
|||||
 |
|||||
| Fig.8 - Símbolo Lógico | |||||
| Fig.7 - Somador Inteiro - Circuito Lógico | |||||
O somador série soma uma coluna de cada vez em sincronismo com o sinal de relógio.As parcelas são carregadas em registradores de deslocamento de n bits e um registrador de deslocamento de n+1 bits receberá a soma.Depois de cada pulso de relógio, os bits das parcelas são colocados na entrada do somador juntamente com o bit de vai-um e, o bit da soma é registrado no registrador de deslocamento da soma.O flip-flop tipo D atrasa o bit de vai-um um período de relógio, de modo que seja somado na próxima coluna de maior significância.
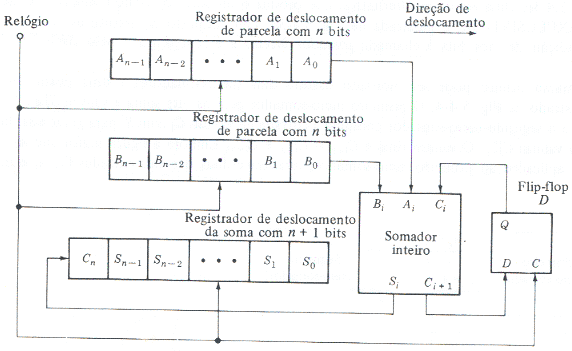
Fig.9 - Somador Série
Para soma dois número de n bits cada, o somador série necessita de n+1 pulsos de relógio.Embora seja econômico em têrmos de circuitos, o somador série é lento.
Somador Paralelo
O circuito da Fig.10 abaixo embora gaste mais somadores, um para cada coluna das parcelas, é masi rápido pois soma todos os bits simultaneamente.É necessário que todos os bits Ai e Bi estejam disponíveis em registradores para serem aplicados nas entradas dos somadores ao mesmo tempo.Isto fornece a soma em um ciclo de relógio, desconsiderando os atrasos de propagação nos somadores.
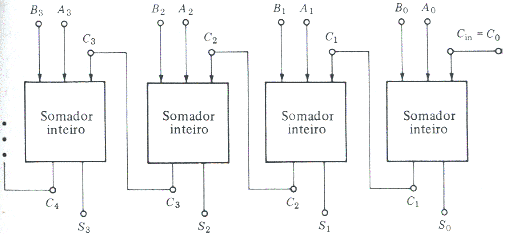
Fig.10 - Somador paralelo
Na realidade, é necessário esperar um determinado intervalo de tempo para que os bits de vai-um se propagarem através de cada somador, antes de considerar válido o resultado da soma na saída.O tempo de propagação do vai-um torna o somador paralelo inaplicável em várias situações.
Considerando que cada porta tem um atraso de propagação igual a um tap, então cada somador atrasa de 2tap.Como para somar duas parcelas de n bits cada, são necessários n somadores, então o resultado da soma somente está disponível na saída em um intervalo de tempo igual a n(2tap).
O atraso do somador paralelo aumenta com o número de bits das parcelas a serem somadas, tornando-o inaplicável para soma de palavras com vários bits de comprimento.
Subtratores
A teoria desenvolvida pode ser usada para desenvolver circuitos meio-somador e somador inteiro. Porém uma vantagem dos somadores é transformar uma operação de subtração em uma operação de soma.Para subtrair um número B de outro número A usando um somador, obtem -B, em seguida, se efetua A+(-B).
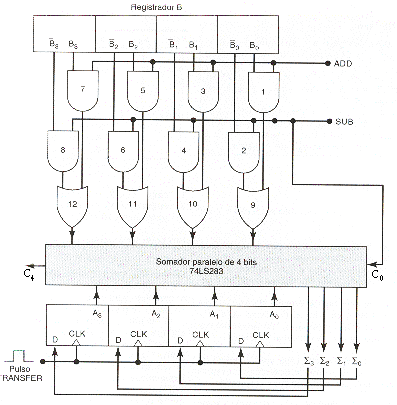
Fig.11- Somador/subtrator em complemento-de-dois
Observe no circuito acima que as portas AND 2, 4, 6 e 8 formam o complemento-de-um da parcela B e, com a entrada SUB=1, C0=1, que soma 1 ao complemento-de-um de B, obtendo o complemento-de-dois de B, ou seja, -B, que somando à parcela A, forma A+(-B)=A-B.
Multiplicação e Divisão Binárias
A multiplicação de números binários é feita da mesma maneira que a multiplicação de números decimais. É maios simples pois o dígito multiplicador é igual a 0 ou 1.
Exemplo. Multiplicação de números binários sem sinal.
| 1 | 0 | 0 | 1 | Multiplicando=9 | |||||||||||||
| 1 | 0 | 1 | 1 | Multiplicador=11 | |||||||||||||
| --------- | |||||||||||||||||
| 1 | 0 | 0 | 1 | ||||||||||||||
| 1 | 0 | 0 | 1 | ||||||||||||||
| 0 | 0 | 0 | 0 | ||||||||||||||
| 1 | 0 | 0 | 1 | ||||||||||||||
| ----------------- | |||||||||||||||||
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | Produto=99 | ||||||||||
Os circuitos digitais aritméticos adicionam somente dois números binários de cada vez, então os produtos parciais são somados dois a dois: o primeiro com o segundo, e o resultado será somado ao terceiro e sucessivamente.
Multiplicação no Sistema de Representação em Complemento-de-Dois
Existem quatro casos diferentes de multiplicação de números binários em complemento-de-dois:
a)Se os dois números são positivos, então a multiplicação é feita como o processo descrito acima. O resultado é positivo e o bit de sinal será igual a 0.
b)Se os dois números são negativos, estarão na forma de complemento-de-dois, então o complemento-de-dois de cada número é calculado para obter os números positivos de cada um e a multiplicação é feita como no processo acima. O produto será um número positivo e o bit de sinal é igual a 0.
c)Se um dos números é negativo e outro positivo, então o número negativo é primeiro convertido para magnitude positiva, através do cálculo do complemento-de-dois correspondente. O produto é feito com os dois números na magnitude positiva e o resultado parcial será positivo. Como os números tem sinais diferentes, então o produto final deve ser negativo, e é obtido calculando o complemento-de-dois do resultado parcial, e o bit de sinal será 1.
O processo de dividir um número(dividendo) por outro(divisor) é o mesmo que feito para números decimais, chamado de "divisão longa". O processo é mais simples pois o divisor só 'cabe' no dividendo 0 ou 1 vez.
Exemplo. Dividir 1001 por 11 que equivale a 9÷3.
| Dividendo=9 | 1 | 0 | 0 | 1 | | | 1 | 1 | Divisor=3 | |||||||||
| |______ | |||||||||||||||||
| 0 | 1 | 1 | 1 | 1 | Quociente=3 | ||||||||||||
| --------- | |||||||||||||||||
| 0 | 0 | 1 | 1 | ||||||||||||||
| 1 | 1 | ||||||||||||||||
| --------- | |||||||||||||||||
| 0 | Resto=0 | ||||||||||||||||
Os casos de divisão binária de números com sinal são os mesmos da multiplicação.
a)Os dois números são positivos então a divisão é feita com descrito acima, o resltado é positivo e o bit de sinal é igual 0.
b)Números negativos são transformados em números positivos por complemento-de-dois e a divisão feita depois.
c)Se o dividendo e divisor tiverem sinais opostos, então o quociente resultante é transformado em um número negativo tomando seu complemento-de-dois e o bit de sinal igual a 1.
d)Se o dividendo e divisor tiverem sinais iguais, então o quociente resultante é um número positivo e o bit de sinal igual a 0.
| Circuitos Integrados Somadores Visite esta página para obter informações sobre o CI somador SN74LS283. |
|||

Atualizada em 28/11/10
