

Representação Digital - uma quantidade é representada por um arranjo de símbolos chamados dígitos.
Diferenças entre Grandezas Analógicas e Digitais
Analógica = Contínua
Digital = Discreta
Sistemas Analógicos e Digitais
Sistema Digital - combinação de dispositivos projetado para manipular grandezas físicas ou informação que são representadas na forma digital, que só podem assumir valôres discretos.
Sistema Analógico - contém dispositivos que manipulam grandezas físicas que são representadas na forma analógica, que podem variar em uma faixa contínua de valôres.
Vantagens das Técnicas Digitais
| - Mais Fáceis de Projetar - Facilidade de Armazenamento da Informação Digital - Maiores Precisão e Exatidão - Operação Programada - Menos Suscetível a Ruídos - Maior Integração dos Circuitos Integrados(CIs) |
Limitação das Técnicas Digitais
O mundo real é principalmente analógico
Variáveis e Funções Lógicas
Variável - letra ou símbolo que pode assumir qualquer valor equivalente a um número de um conjunto de números, quando o conjunto contém mais de um número.
Campo de uma Variável - intervalo de valôres que pode ser assumido por uma variável.
Função - regra(relação) da qual se determina o valor de uma segunda variável (dependente) do valor da variável independente.
Variáveis Lógicas
Uma variável lógica deve apresentar as três propriedades abaixo:
Valôres de Uma Variável Lógica
Uma variável lógica A tem ou um valor verdadeiro(A=V) ou o valor falso(A=F).
Funções de Uma Variável Lógica
As funções possíveis de uma variável lógica, representadas por Z=f(A), são dadas pelas Tabelas Verdades da Fig.1.
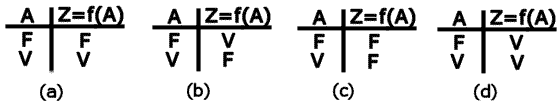 |
Nas Tabelas verdades (c) e (d), os valôres de Z independem dos valôres assumidos por A.
Funções de Duas Variáveis Lógicas
Função AND(E):
Z=f(A,B) somente é verdadeira quando A e B são ambas verdadeiras.
A tabela verdade da função AND(E) é mostrada na Fig.2.
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
| Fig.2 |
|
||||||||||||||||||||||
Função OR(OU):
Z=f(A,B) somente é verdadeira quando uma das variáveis ou ambas são verdadeiras.
A tabela verdade da função OR(OU) é mostrada na Fig.3.
|
Fig.3 |
|
Representação de Variáveis Lógicas por Tensões Elétricas
Em geral, usa-se uma faixa de tensão para representar o valor falso ou verdadeiro de uma variável lógica.
Lógica Positiva - a tensão mais positiva representa o valor V e a mais negativa o valor F.
Lógica Negativa - o valor V é representado pela tensão mais negativa e F pela tensão mais positiva.
Lógica Mista - no mesmo sistema, usa-se as lógicas positiva e negativa.
Porta Lógica - estrutura que gera uma função lógica Z.
Símbolos
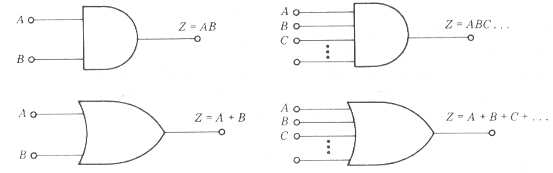 |
A Fig.4 mostra os símbolos lógicos para as portas lógicas AND e OR.
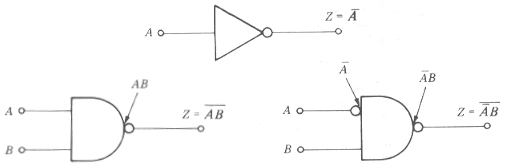
Inversão - Função NOT(NÃO)
Inversor - porta lógica com uma única entrada e uma única saída, que é a inversão lógica(complemento) da entrada.
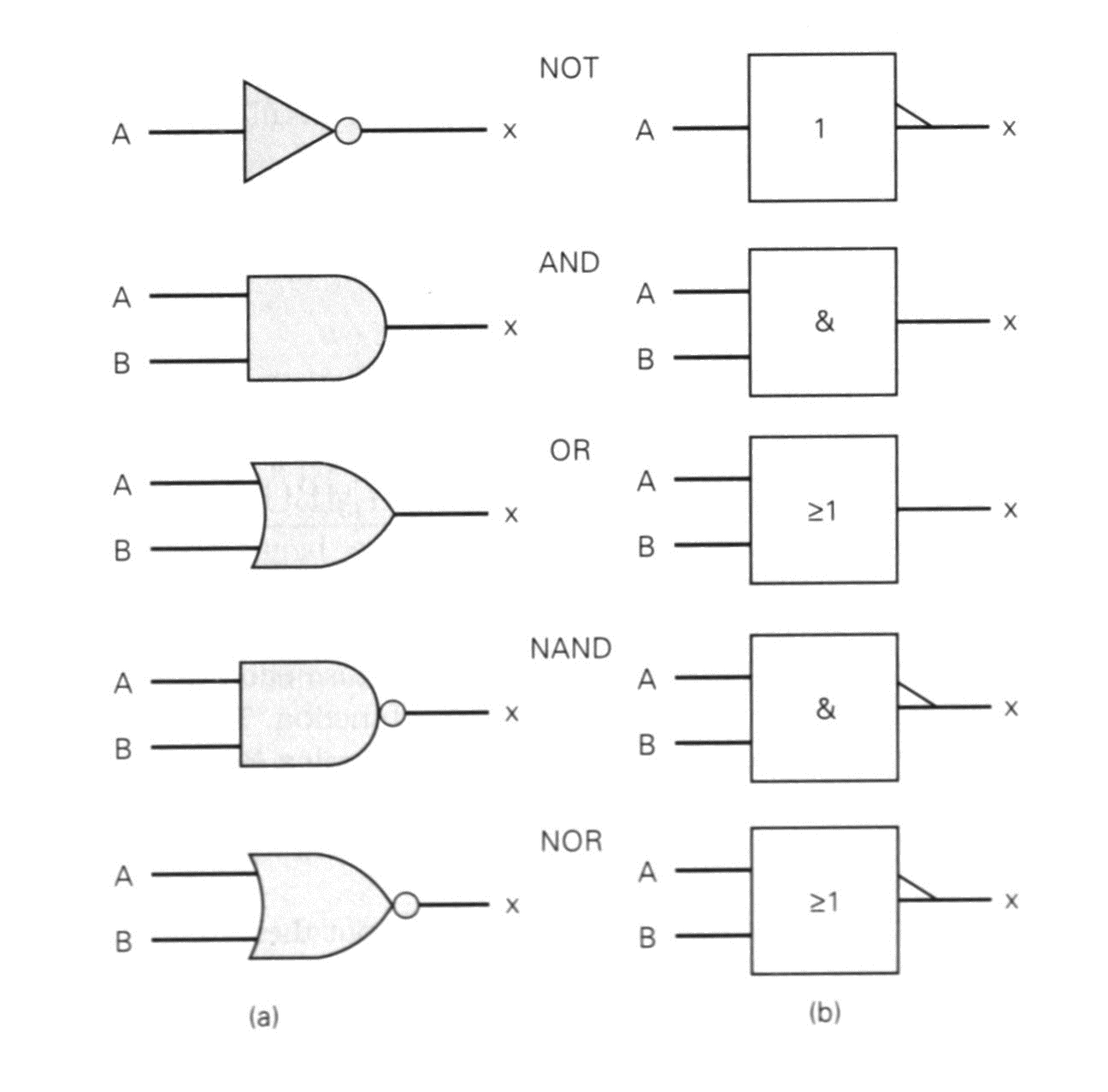
A Fig.5 mosta o símbolo lógico da porta INVERSOR e o emprego em outras estruturas. Os símbolos das portas lógicas apresentados são os símbolos usados pela maioria dos livros e indústria. Esta simbologia útil para representar portas lógicas não funciona adequadamente para CIs complexos com várias entradas e saídas.
A norma técnica IEEE/ANSI 91-1984 padronizou um novo conjunto de símbolos lógicos e a notação de dependência para CIs. A Fig.5 mostra os novos símbolos.
 |
 |
| Fig.5 |
| Questões de Revisão - Funções Lógicas Verifique seus conhecimentos e resolva esse Teste sobre funções lógicas. |
Notação 0 e 1
Para uma variável lógica com valor VERDADEIRO(V) emprega-se A=1 e para valor FALSO(F) da variável lógica A, usa-se A=0.
Observe que 0 e 1 não são números, mas valores lógicos de uma variável lógica.Então, as funções AND e OR ficam com as seguintes tabelas verdades:
| Função AND: | Função OR: |
|
||||||||||||||||||||||||||||||
|
|
Álgebra de Boole
Teoremas da Álgebra de Boole
Princípio da Dualidade - em uma equação lógica, se trocar (+) por (.), (.) por (+), 0s por 1s, e 1s por 0s, então substitui-se a equação original por outra igualmente válida.
Teoremas Duais - teoremas obtidos trocando as operações (+) por (.), (.) por (+) e 0s por 1s, 1s por 0s; as expressões derivadas são chamadas duais uma da outra.
| Teoremas | ||||||
| I. O complemento do complemento de uma variável lógica A é a própria variável A. |
||||||
| Fig.6 |
||||||
| II. Teoremas de uma única variável. |
III.Teoremas de duas e três variáveis sob a forma de pares duais. |
|||||
|
|
Fig.7 | ||||
 |
![]()
Fig.9a
(2) o complemento de uma soma de variáveis é igual ao produto dos complementos de cada uma das variáveis.
![]()
Fig.9b
As Funções de Duas Variáveis
Existem dezesseis funções de duas variáveis, das quais examinamos acima as funções AND, OR e
NOT. Agora examinaremos as funções restantes, particularmente aquelas que interessam à eletrônica digital. A tabela abaixo mostra todas as dezesseis funções, com destaque para aquelas de interesse.
| Função | |||||
| f=0 | |||||
| f=A AND B | |||||
| f=A NOT-IMPLIES B | |||||
| f=A | |||||
| f=B NOT-IMPLIES A | |||||
| f=B | |||||
| f=A X-OR B | |||||
| f=A OR B | |||||
| f=A NOR B | |||||
| f=A X-NOR B | |||||
| f=NOT B | |||||
| f=B IMPLIES A | |||||
| f=NOT A | |||||
| f=A IMPLIES B | |||||
| f=A NAND B | |||||
| f=1 |
A Função EXCLUSIVE-OR(X-OR)
A função EXCLUSIVE-OR(OU-EXCLUSIVO), f6, fornece saída igual a valor lógico 1 se uma das variáveis de entrada A ou B, na exclusão da outra variável, tiver valor lógico 1.
| Tabela Verdade | Representação | Propriedades | ||||||||||||||||||
|
|
Símbolo da porta lógica X-OR:

Fig.11
A Função EXCLUSIVE-NOR(X-NOR)
A função EXCLUSIVE-NOR(NOR-EXCLUSIVO), f9, fornece saída igual a valor lógico 1 se as duas variáveis de entrada A e B tiverem valores lógicos iguais. Esta função é também chamada função EQUIVALÊNCIA .
| Tabela Verdade | Representação | Propriedades | ||||||||||||||||||
|
Símbolo da porta lógica X-NOR
 :
:
Fig.12
As Funções NAND e NOR
A Função NAND:
Z=f(A,B)=A NAND B somente é 0 quando A e B são ambas iguais a 1.
A tabela verdade da função NAND é mostrada abaixo.
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||
|
|
Símbolo da porta lógica NAND:
![]()
A Função NOR:
Z=f(A,B)=A NOR B somente é 1 quando A e B são ambas iguais a 0.
A tabela verdade da função NOR é mostrada abaixo:
| Tabela Verdade | Representação | Propriedades |
|
||||||||||||||||||
|
|
Símbolo da Porta Lógica NOR:
![]()
| Questões de Revisão - Funções lógicas NAND e NOR. Resolva esse Teste sobre as funções NAND e NOR. |
Representação Alternativa das Portas Lógicas
Regras para obter a representação alternativa das portas lógicas:
1.Inverta cada entrada e saída do símbolo padrão da porta lógica
2.Trocar todas as operações AND por OR e, todas as operações OR por AND;
3.O símbolo da operação INVERSOR permanece inalterado.
A Fig.13 mostra os símbolos padrões de representação das portas lógicas e as correspondentes representações alternativas.
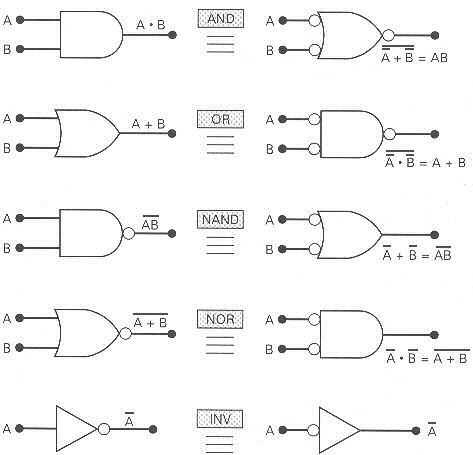
Fig.13
Algumas propriedades podem ser observadas nas representações das portas lógicas:
a) a equivalência pode ser estendida para portas com qualquer número de entradas;
b) nenhum símbolo padrão tem inversão na entrada; todos os símbolos alternativos tem inversão na entrada;
c) os símbolos padrão e alternativo de cada porta representam o mesmo circuito físico; não há diferenças no circuito representado pelos dois símbolos;
d) NAND e NOR são portas inversoras, assim os símbolos lógicos padrão e alternativo tem inversores na saída, ou na entrada; AND e OR são portas não inversoras, assim os símbolos lógicos padrão e alternativo tem inversores na entrada e saída.
Para determinar o símbolo lógico alternativo para uma porta lógica, no símbolo lógico padrão troque as operações OR por AND, ou AND por OR, e substitua as inversões nas entradas e saídas (apague as inversões onde existem e acrescente onde não existem).
Interpretação do Símbolo Lógico
Nível lógico ATIVO ALTO - quando a linha de entrada ou saída do símbolo lógico de um circuito lógico não tem inversão.
Nível lógico ATIVO BAIXO - quando uma linha de entrada ou saída do símbolo de um circuito lógico tem inversão.
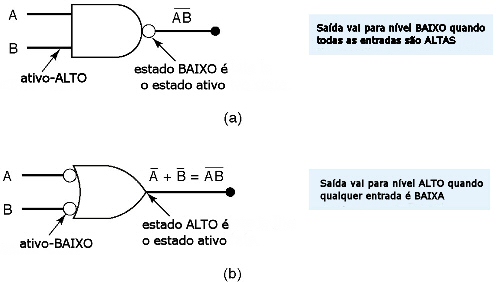
Fig.14
Para determinar oa níveis lógicos ATIVOS para as entradas e saídas de uma porta lógica, basta observar que se símbolo lógico AND é usado, então a saída é ATIVA se todas as entradas são ATIVAS; se um símbolo OR é usado, então a saída é ATIVA se qualquer entrada é ATIVA.
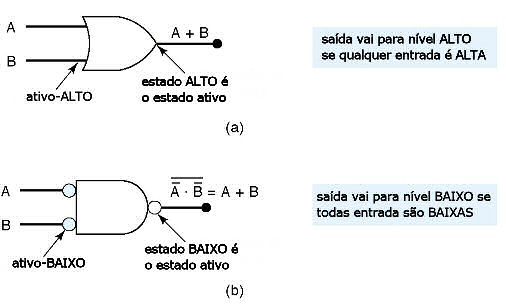
Fig.15
A representação a ser usada é determinada pela aplicação da saída do circuito; se a saída deve provocar alguma ação no nível ALTO, então se usa a representação com a saída ALTA; se a ação é ativada por nível BAIXO, então é empregada a representação com saída BAIXA.
Na Fig.16, temos as duas possibilidades de representar o mesmo circuito lógico.O circuito da Fig.16(a) tem a tabela verdade apresentada na Fig.16(d). Na Fig.16(b), o circuito fornece saída ativa ALTA e, na Fig.16(c), o circuito foi redesenhado para fornecer saída ativa BAIXA.
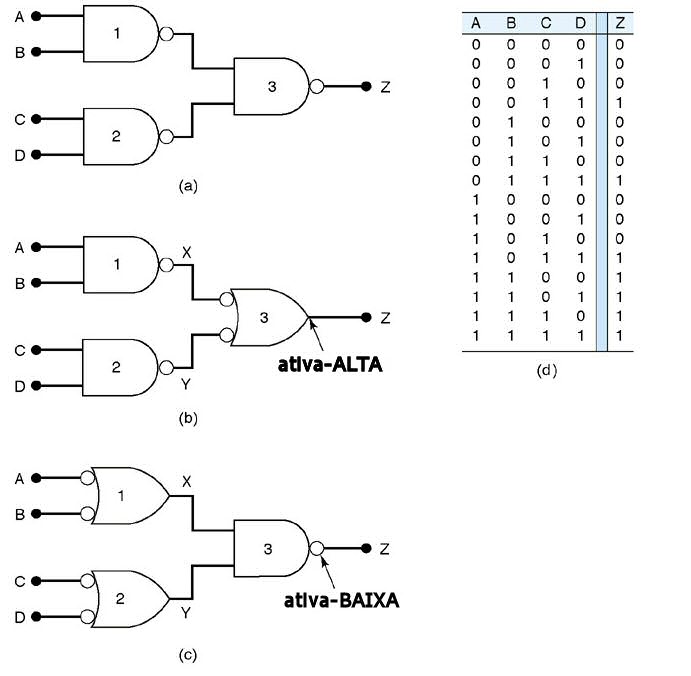
Fig.16
Sempre que fôr possível, usar os símbolos lógicos das portas de modo que as saídas com inversão sejam ligadas a entrada com inversão, e saídas sem inversão conectadas a entradas sem inversão.
Quando um sinal lógico se encontra no seu estado ativo, então se diz que o sinal está ATIVADO(ASSERTED). Quando um sinal lógico não está no seu estado ativo, então o sinal está DESATIVADO(UNASSERTED).
As designações dos sinais lógicos ativos BAIXOS devem ter uma barra sobre os nomes para indicar um sinal ativo BAIXO. Para sinais lógicos com dois estados de atividade, então o nome deve indicar quais são os níveis de atividade dos dois estados.
Na Fig.17 abaixo, a saída MEM é usada para ativar CIs de memórias em determinado microcomputador, a partir dos sinais de entrada RD, ROM-A, ROM-B, e RAM.
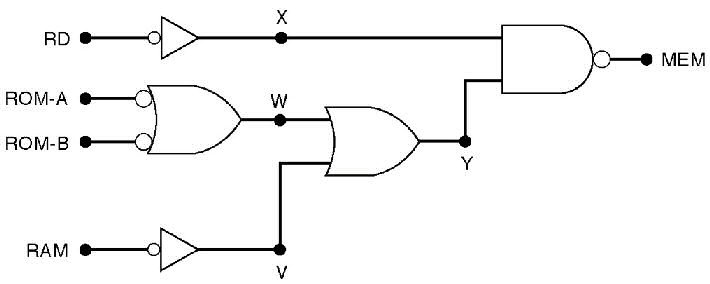
Fig.17
Uma maneira de determinar a expressão para MEM é escrever uma tabela verdade e avaliar as dezesseis combinações das entradas. Embora eficiente, este método poderia ser mais trabalhoso. Uma maneira mais rápida é analisar o diagram do circuito empregando os níveis de atividades dos sinais.
1.MEM é ativo BAIXO, e vai para o nível BAIXO quando X e Y são ambos ALTOS.
2.X será ALTO somente quando RD fôr BAIXO.
3.Y será ALTO quando ou W fôr ALTO ou V fôr ALTO.
4.V é ALTO quando RAM fôr BAIXO.
5.W será ALTO se ROM-A ou ROM-B fôr BAIXO.
6.Então, MEM vai para o nível BAIXO quando RD é BAIXO, e, no mínimo, uma das entradas ROM-A, ROM-B ou RAM é BAIXA.
O circuito lógico da Fig.18 é usado para controlar a rotação de um motor da unidade de disco quando o microcomputador está recebendo ou enviando dados para o disco.O circuito ligará o motor quando o sinal de saída DRIVE é ALTO.
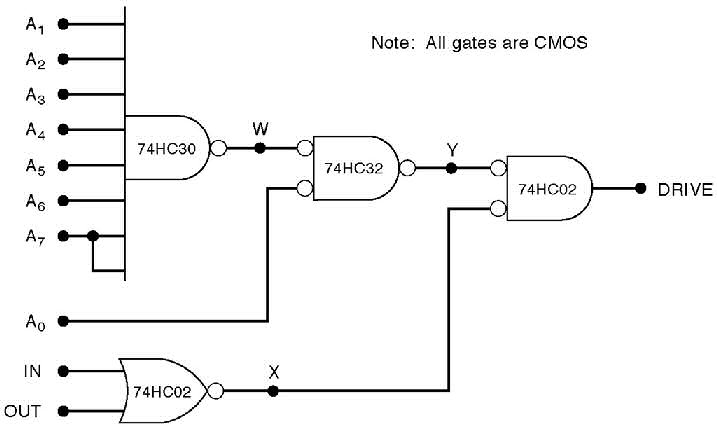
Fig.18
As condições dos sinais de entrada necessárias para ligar o motor podem ser determinadas a partir da análise dos níveis de atividade dos sinais de entrada e saída do circuito.
1.DRIVE é ativo ALTO vai para o nível ALTO se X e Y forem BAIXOS.
2.X será BAIXO se IN ou OUT é ALTO.
3.Y será BAIXO quando W e A0 forem ambos BAIXOS.
4.W será BAIXO somente quando A1 até A7forem ALTOS.
5.Resumindo, temos: DRIVE será ALTO quando A1=A2=A3=A4=A5=A6=A7=1(ALTO) e A0=0(BAIXO), e IN ou OUT ou ambos forem iguais a 1(ALTO)
Suficiência das Operações NAND e NOR
A operação NOT, juntamente com a operação AND ou juntamente com a operação OR, é suficiente para expressar qualquer função lógica.Esta propriedade é consequência direta da relação entre as funções de duas variáveis e as funções NOT, AND e OR, que podem expressar qualquer outra função.
Suficiência de NAND
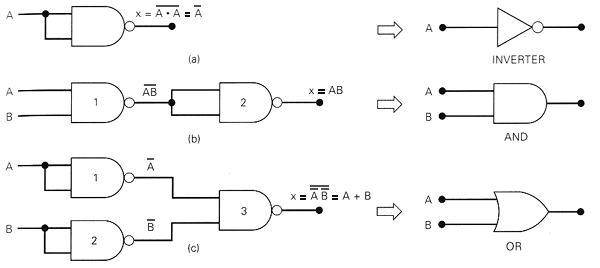
Fig.17
Suficiência de NOR
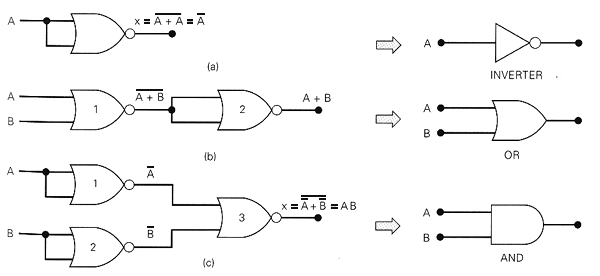
Fig.18
Questões de Revisão - Álgebra das Variáveis Lógicas e Teoremas de Boole |

Atualizada em 15/02/12
