

Base: 16 |
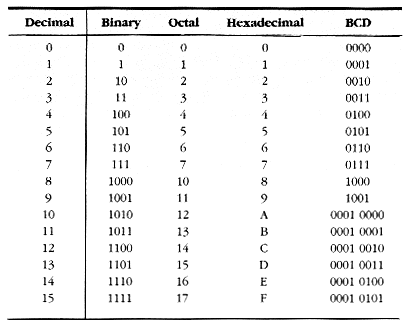 |
|
||
| Fig.1 |
|
|||
| Dividendo | ||||||
| Resto |
| 0,69 X 2 = 1,38 | 1 | MSB |
| 0,38 X 2 = 0,76 | 0 |
|
| 0,76 X 2 = 1,52 | 1 |
|
| 0,52 X 2 = 1,04 | 1 |
LSB |
| 0,6910 = 0,10112 |
||
| 19,6910 = 10011,10112 |
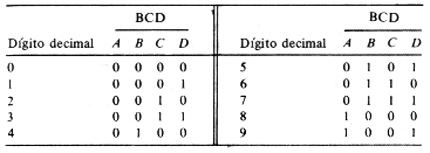
BCD |
0101 |
0100 |
0010 |
0111 |
|
A Fig.3 mostra a formação do Código Refletido para os números decimais de 0 a 7. Propriedades. |
|||
| Fig.3 | ||||
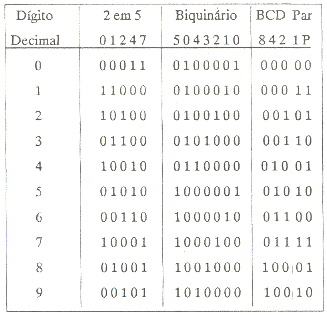 |
Nestes códigos, a deteção do erro é feita pelo teste da paridade da palavra.Adiciona-se dígitos extras às palavras de modo que o números 1 na palavra seja par(ou ímpar).Em todos os exemplos da Fig.7 a paridade é par. |
Fig.7 |
|
Em qualquer um dos três exemplos, a ocorrência de um erro simples transforma o arranjo válido em outro inválido, possibilitando a deteção do erro. |
|
H= |
1 |
0 |
1 |
||
0 |
1 |
1 |
H= |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|||
0 |
0 |
1 |
1 |
1 |
0 |
1 |
G= |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
||
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|||
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|||
1 |
1 |
1 |
0 |
0 |
0 |
1 |
Dígito Decimal |
Código Hamming |
||||||
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
v7 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
4 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
7 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
8 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
[1 0 0 1 1 0 1]. |
|
| Questões de Revisão Resolva on-line questões sobre sistemas numéricos, conversão entre sistemas numéricos, códigos e deteção e correção de erros. |

Especificações detalhadas e tolerâncias dos vários códigos de barras não existem. A falta dessas especificações possibilita amplas variações em um código de barras simples.Como resultado, qualquer scanner de código de barras deve ser projetado para manipular as diversas variações do código de barras.
- MSI
- UPC(Universal Product Code)
- EAN(European Article Number)
- CODABAR
- 2-of-5
- 2-of-5-Interleaved
- Code 39
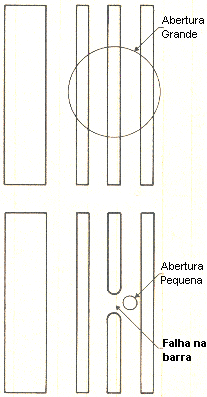
| Na figura temos dois tipos de abertura: na superior, um leitor com abertura grande e, na inferior, o leitor tem uma pequena abertura. Se abertura do leitor fôr muito grande e as barras com larguras muito estreitas, então pode ocorrer que o scanner não reconheça as barras.Por exemplo, se as barras têm larguras iguais a 4X10-3 polegadas(aproximadamente, 9mm) e abertura do leitor é 10X10-3 polegadas (em torno de 22,5mm), então 60% da abertura refletirá a luz dos espaços em branco ao lado de cada barra.A luz detectada pode não diminuir para um nível que permitirá a barra ser reconhecida. Contraste ou tolerância de reconhecimento e consumo de potência formam o critério de seleção para a escolha da abertura de um scanner em relação a determinado código de barras. Então, a abertura do leitor deve ser bastante pequena para reconhecer as barras e larga o suficiente para tolerar erros de impressão. O consumo de potência óptica deve ser aceitável para aplicação desejada. |
 |
|
|
Fig.9 |
|
||
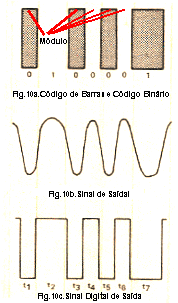 Fig.10 Fig.10 |
Quando o leitor é movimentado sobre o código de barras, como mostrado na Fig.10a, o sinal elétrico é produzido pelo scanner apresenta a forma da Fig.10b.Esse sinal é convertido para o sinal digital mostrado na Fig.10c, e interpretado para determinar o caractere apropriado representado pelo código de barras. Cada espaço claro e escuro no código de barras é igual ou maior que uma unidade de tamanho chamado módulo. Períodos de sinais elétricos não são medidos em termos de polegadas ou centímetros, mas em termos de tempo.Para produzir o sinal, o scanner é movimentado através do código de barras com certa velocidade.Se a velocidade do scanner fôr conhecida e constante, o sinal poderia ser dado em polegadas ou centímetros com precisão.As larguras das barras e espaços então seriam determinadas e comparadas.Desde que a velocidade do scanner não é conhecida, a largura de espaços e barras é expressa como uma função do tempo.A velocidade do scanner nem é conhecida nem constante sobre o código de barras.Mesmo que a velocidade do scanner fôsse constante, dimensões de larguras diferentes entre diferentes tamanhos de códigos de barras poderiam produzir sinais de larguras variáveis em termos de tempo. Uma velocidade de 76 a 760mm/s é tolerável para maioria dos operadores e tipos de códigos. |
|

Atualizada em 30/08/11
