Eletrônica Digital - Formas Padrões das Funções Lógicas

Soma Padrão de Produtos
Qualquer função lógica pode ser expressa como uma soma de produtos(SOP - Sum Of Products), isto é, várias operações AND cujas saídas são entradas de uma operação OR.

Exemplo.

A inversão na soma de produtos não pode ser em mais de uma variável em um têrmo AND.
Uma função na forma padrão de soma de produtos, cada têrmo produto contém cada uma das variáveis (complementadas ou não-complementadas).
Exemplo.

Mintermo(m) - produto da soma padrão de produtos contendo cada uma das variáveis da função, complementadas ou não-complementadas.
Número do mintermo - número decimal obtido atribuindo 0 a cada variável complementada e 1 a cada variável não-complementada em determinado mintermo.
Para a função acima temos:

Então,

Produto Padrão de Somas
Qualquer função lógica pode ser expressa como um produto de somas(POS- Products of Sum), isto é, várias operações OR cujas saídas são entradas de uma operação AND.
Exemplo.

Em cada têrmo soma, a inversão só pode ser em uma única variável.
Uma função na forma padrão de produtos de somas cada parêntese contém todas as variáveis da função (complementadas e não-complementadas).
Exemplo.

Maxtermo(M) - é cada uma das somas do produto padrão de somas contendo cada uma das variáveis (complementadas e não-complementadas) da função.
Número do Maxtermo - é o número decimal obtido associando 1 à variável complementada e 0 à variável não-complementada de determinado maxtermo.
Para a função do exemplo anterior, temos:

Então, temos

Especificação de Funções com Mintermos e Maxtermos
(a)Expressar a função como padrão de soma de produtos(ou produto de somas)
(b)Ordenar os mintermos(maxtermos) em ordem de numeração crescente
(c)Substituir cada mintermo(maxtermo) por sua representação
(d)Compactar a soma(produto) das representações como um somatório(produtório)

Relação Entre Mintermos, Maxtermos e a Tabela Verdade
Uma função expressa na forma de soma de mintermos deve incluir os mintermos cujos números correspondem às linhas na tabela verdade onde a função tem valor lógico 1.
Uma função expressa na forma de produto de maxtermos, o número de maxtermos que devem ser incluídos correspondem aos das linhas da tabela verdade onde a função tem valor lógico 0.
Exemplo.

fig9
Fig.15

Estruturas de Dois Níveis de Portas
Estruturas resultantes da implementação física de uma função expressa como soma de produtos ou produto de somas(não-padronizadas). Uma variável lógica deve passar através de duas portas antes que seu efeito seja sentido na saída.
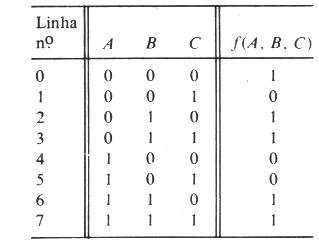
Exemplos.

Atraso de Propagação da Porta - tempo decorrido entre a variação de tensão na entrada da porta e a correspondente alteração de tensão na saída, se houver.
As estruturas de dois níveis minimizam os atrasos; é necessário que certas variáveis estejam disponíveis na forma complementada e não-complementada.

Estruturas Usando um Tipo de Porta
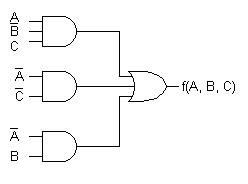
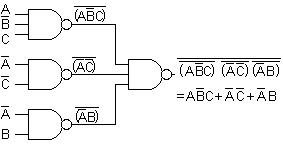
Conversão de estruturas de dois níveis de portas AND-OR para estruturas com portas NAND.

fig17

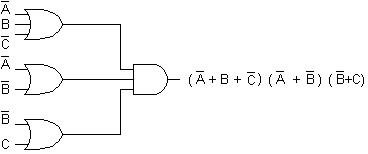
Conversão de estruturas de dois níveis com portas OR-AND para estruturas com portas NOR.

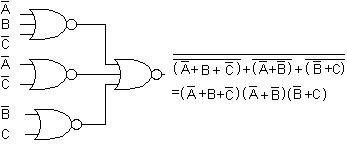
fig20

Resumo

         Estruturas com portas NAND
         (a) Expressar a função como uma soma de produtos
         (b) Desenhar a estrutura de dois níveis com portas AND-OR
         (c) Substituir todas as portas AND-OR por portas NAND

         Estruturas com portas NOR
         (a) Expressar a função como um produto de somas
         (b) Desenhar a estrutura de dois níveis com portas OR-AND
         (c) Substituir todas as portas OR-AND por portas NOR

Questões de Revisão
Resolva on-line questões sobre as formas padrão das funções lógicas e estruturas com dois níveis de portas.