
1. Figure 1.1 shows a smooth box in which a small block of mass m is connected by two identical light springs to opposite sides, A and B, of the box.

Initially both springs are stretched an equal amount e and the force constant is 10 Nm-1
each. The block is now displaced a small distance along AB from the equilibrium position and is released from rest. (Assume that both springs are always in tension. )
(a) When the block is at a distance x from the equilibrium position, write down the expressions for the tensions, T1 and T2 in the springs. Show that the motion of th block is simple harmoic. ( 4 marks )
(b) Figure 1.2 shows the time variation of the potential energy of one of the springs.
Fig. 1.2 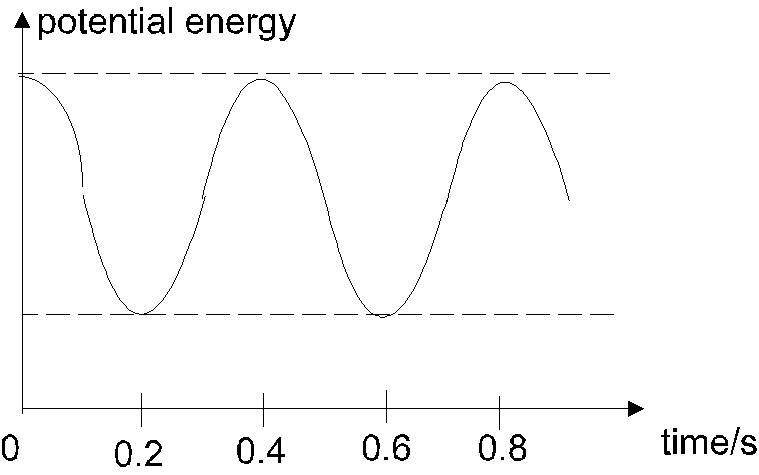
(i) Using crosses, indicate on the graph the points corresponding to the time at which the block at its extreme positions. (1 mark )
(ii) Find the period of oscillation and the mass of the block. ( 4 marks )
(c) State the change , if any , in the period of oscillation if
(i) the box is tilted at a small angle to the horizontal; (1 mark )
(ii) a large box with greater separation AB is used. ( 1 mark )
2. A small source emitting electromagnetic waves of frequency 1010 Hz is placed some distance, say 100 m, from a 1 m ´ 1m , square metal plate. The line joining the source and the centre of the plate is perpendicular to the plate. Figure 2.1 shows part of the waveforms emitted from the source towards the plate.
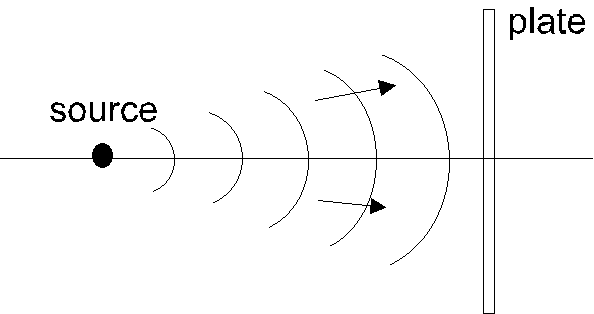
(a) Name the electromagnetic waves emitted. ( 1 mark )
(b) (i) In Figure 2.1, sketch the reflected wavefronts and indicate the position S’ where the reflected wavefronts appear to come from. ( 2 marks )
(ii) A detector registers a non-zero reading when it is placed some distance behind the plate on the line joining the source and the centre of the plate. Briefly explain this observation with the aid of a diagram. ( 2 marks )

(c) (i) If the plate is now moving towards the source at a speed of 20 m/s, what would the speed of position S’ in (b) (I) be ? Hence or otherwise calculate the change in frequency of th reflected waves. ( 3 marks )
(ii) A typical radar speed trap employs similar principles by sending some electromagnetic waves towards a moving car. To deduce the speed of the car, the reflected waves received are compared with the emitted waves in such a way that the beat frequency between them ca be measured. Explain why the car frequency is measured instead of the reflected waves being directly measured. ( 2 marks )
3. Figure 3.1 shows a uniform uire which is held taut but unstretched between a fixed point and a smooth cylindrical peg of radius 1 cm. The force constant of the wire is 9.6 ´ 102 N m-1. The tension in the wire can be increased by rotating the peg about its fixed axis so that some wire is wound onto the peg.
Figure 3.1 
(a) When the peg is rotated through an angle of 2p ,calculate
(i) the tension in the wire. ( 2 marks )
(ii) the work done in rotating the peg. ( 2 marks )
(b) The above wire is part of a musical instrument. Two knife edges, A and B, are placed 0.36 m apart under the stretched wire as shown in Figure 3.2. The mass of the wire between A and B 6.4 ´ 10-4 kg. ( Assume that the presence of the two knife edges would not affect the tension in the wire. )
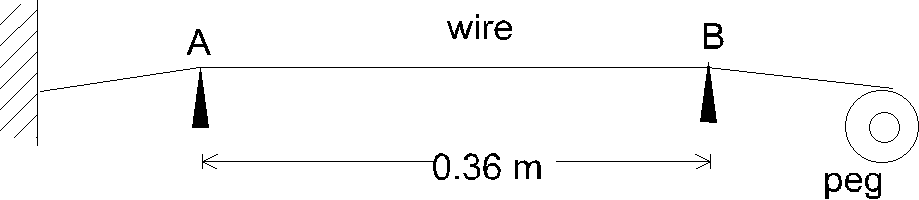
(i) Calculate the frequency of the fundamental note emitted when the wire between A and B is plucked. ( 3 marks )
(ii) State THREE differences between the waves in the wire and the fundamental note emitted. ( 3 marks )
(iii) Draw a diagram to show the vibration of the wire between A and B when it is vibrating at the third harmonic. ( 1 mark )
4. (a) Figure 4.1 shows three identical cells connected with a 10-kW resistor. A student uses a CRO and a moving-coil voltmeter in turn to measure the potential difference across PQ, the readings being 4.5 V and 4.1 V respectively.
Figure 4.1 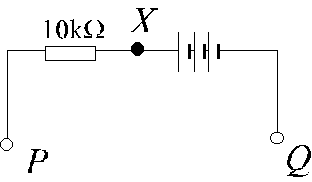
(i) Account for the difference in the readings, (3 marks)
(ii) Estimate the resistance of the voltmeter. What would the reading be if the voltmeter is connected across XQ ? (3 marks)
(b) Figure 4.2 shows part of the internal structure of a typical multimeter. It has a coil connected to a shunt built from resistors R1 and R2, and a series of voltage multipliers R3 and R4.The resistances of R1, R2 and R3 are 9.8 kW , 200 W and 48 kW respectively. A.rotary switch S enables the various full-scale values of current or voltage to be chosen.
Figure 4.2
(i) Calculate the resistance of the coil and the current flowing through it for full-scale deflection. Show your working. (4 marks)
(ii) Calculate the resistance of R4. (2 marks)
(iii) In the spaces provided in Figure 4.2, add two components to the circuit so that the multimeter can be used to measure resistance between its input terminals when switch
S is set at X. Describe briefly how to adjust for zero ohm position. (3 marks)
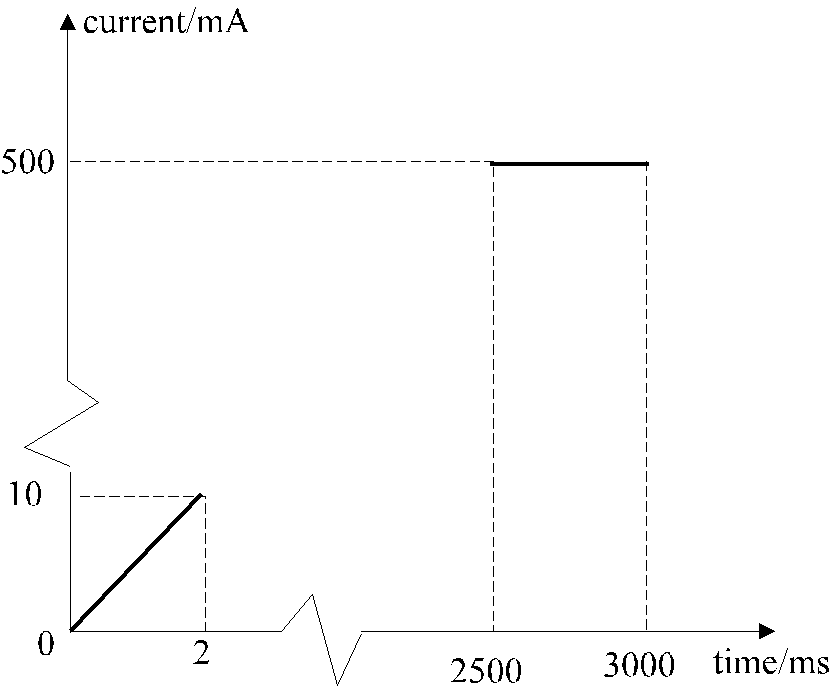
5. An iron-cored inductor L, a milliammeter A and a 9 V d.c. supply of negligible internal resistance are connected as shown in Figure 5.1. The graph shows the variation of current with time during the first few milliseconds, OA, and a few seconds later, BC, after closing switch S
Figure 5.1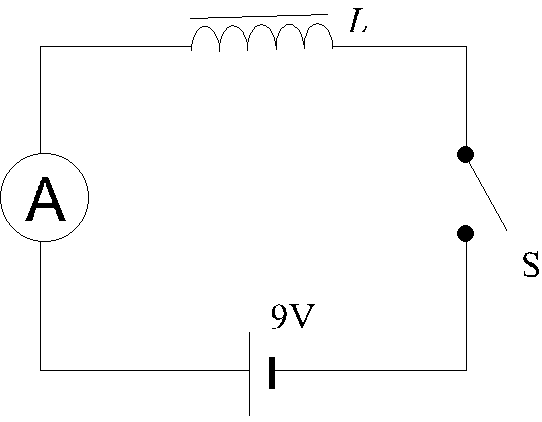
(a) What is meant by the inductance of an inductor ? (1 mark)
(b) (i) Explain why the current cannot rise instantaneously to the final steady value. (2 marks)
(ii) Find the inductance oft. (2 marks)
(iii) Calculate the resistance of the circuit. (2 marks)
(iv) If the soft iron core of inductor L is removed, sketch on the same graph the parts corresponding to OA and BC. (2 marks)
(c) When the circuit is broken by opening switch S, sparking occurs at the contacts of the switch.
(i) Where does the energy for the sparks come from ? · (1 mark)
(ii) In order to prevent sparking, a capacitor is now connected in parallel with the switch. It is known that sparking occurs when the voltage across the contacts of the switch exceeds 350 V. Assuming that the energy loss due to the resistance of the circuit is negligible, calculate the minimum capacitance required to prevent sparking. (3 marks)
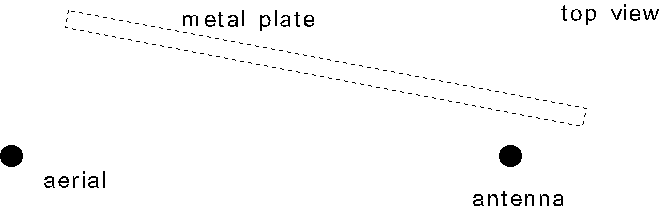
6. (a) Figure 6.1 shows the apparatus for investigating the ~ansmission and reception of 1 Ghz radio waves. A transmitting aerial connected to asignal generator emits plane-polarized radio waves. An antenna connected to a microammeter is used for receiving the radio waves. The antenna can be rotated about its centre in the plane containing it as shown.
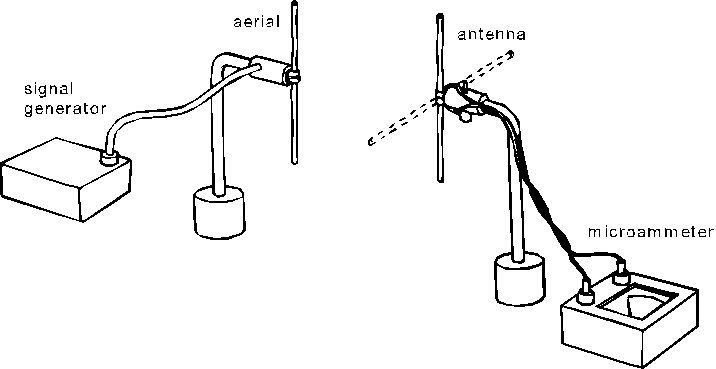
(i) What doyou understand by 'plane-polarized' radio waves? (1 mark)(ii) Describe how you would use the apparatus to show the transverse nature of radio
waves. Explain briefly.
(iii) A metal plate is now placed vertically to one side olthe aerial and the antenna such
that it is very close to the antenna but without touching it. Explain carefully the
change, if any, in the microammeter reading after the plate is placed. (3 marks)
(b) Figure 6.3 shows a simplified tuning circuit for a radio receiver.
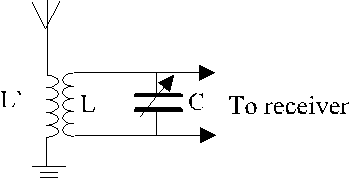
(i) Explain the function of coil L'. (2 marks)(ii) Explain how a radio signal of a particular frequency can be picked up by the LC
circuit though radio signals of various frequencies are received by the antenna.
(2 marks)
(iii) It is preferable to keep the length of the wire for making coil L as short as possible. Briefly explain why this is so. (2 marks)
(b) Figure 6.3 shows a simplified tuning circuit for a radio receiver.
(I) Explain the function of coil L’. (2 marks )
(ii) Explain how a radio signal of a particular frequency can be picked up by the LC circuit though radio signals of various frequencies are received by the antenna.
(iii) It is preferable to keep the length of the wire for making coil L as short as possible. Briefly explain why this so. ( 2 marks )
7. (a)
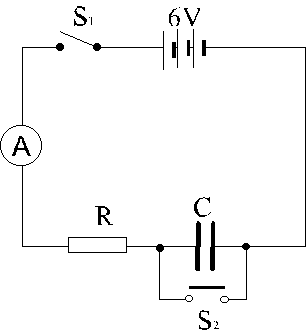
Figure 7.1 shows a circuit used for investigating the charging process of a capacitor. Before the experiment, push-button switch S2 is closed momentarily. With switch S1 closed, the charging process starts. The ammeter readings, I, at various times, r, are taken. The results are plotted on the graph below.
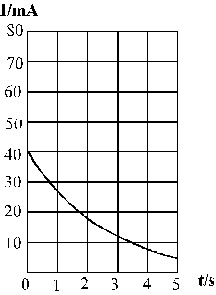
(i) Explain why the ammeter reading decreases with time. (2 marks)
(ii) What is the physical meaning of the area under the curve ? (1 mark)
(iii) Sketch on the same graph to show how the current varies with time when the
experiment is repeated with
(I) a second identical capacitor connected in parallel with C, (label it as curve (I))
(II) a second identical resistor connected in series with R (label it as curve (II)), (4 marks)
(b) Two parallel-plate capacitors, C1 and C2, formed by identical metal plates are connected inseries with an E.H.T. of 1.5 kV as shown in Figure 7.2. Point R of the circuit is earthed. The plate separation of C1 is double that of C1.
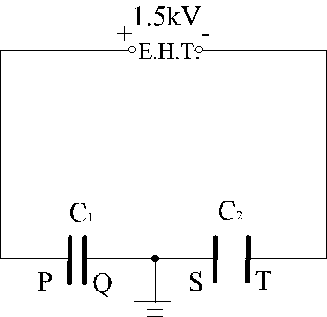
(i) Sketch a graph to show the variation of elecuic potential with position along PQRST. Label both axes. (3 marks)
(ii) Describe and explain what would be observed if a positively-charged foil strip is
moved between the plates of CI without touching them. (3 marks)
(iii) Comparing with (b) (ii), state the change (s), if any, when the foil strip is placed between the plates of C2.
8. Figure shows a device for accelerating protons to a high speed in vacuum. It consists of two semi - circular dees which a uniform magnetic field, B , is present . A p.d. , V , is set up across the narrow gap between the chambers such that its polarities reverse every time the proton goes from one dee to the other.
When a proton of negligible speed is injected into the centre of the device, it is accelerated by the p.d. towards one dee and describes a semi - circle inside that dee due to the magnetic field present. The proton is then accelerated across the gap through a p.d. of V and describes another semi - circle of greater radius in the other dee since its speed has increased. This process is repeated and the path of proton is shown in the figure.
(a) (i) Indicate in the figure the direction of the magnetic field in the dees.
(1 mark)
(ii) For a proton of mass m and charge q moving with speed v in a circle of radius r in one of the dees, express v in terms of r . Explain why the proton does not gain kinetic energy in the dees.
(3 marks)
(iii) Show that the time spent by the proton in describing any semi - circle is independent of v and r .
(2 marks)
(b) It is known that the strength of the magnetic field , B , is 1.5 T and the alternating p.d. , V , is 10 k V.
(Given : electronic charge = 1.60 x 10-19 C ; mass of proton = 1.66 x 10-27 kg )
(i) Find the gain in kinetic energy , in eV , of the proton in each complete revolution.
(1 mark)
(ii) Calculate the time taken for a proton to gain a kinetic energy of 1 M eV .
(3 marks)
(c) In practice, the protons have different initial velocity after the injection, some of these protons will not in phase with the alternating p.d. across dees. Describe what will happen to them
(2 marks)
9.
(a) An operational amplifier of open-loop voltage gain 105 operates with supply voltage ± 15 V. What is the voltage across its input terminals when it has just been saturated ? (1 mark)
(b) (i) In the space provided, draw the circuit ofa voltage follower using an ideal operational amplifier. (2 marks)
(ii) Explain why, for a voltage follower, the output voltage follows the input voltage
exactly. State one application of such a circuit. (3 marks)
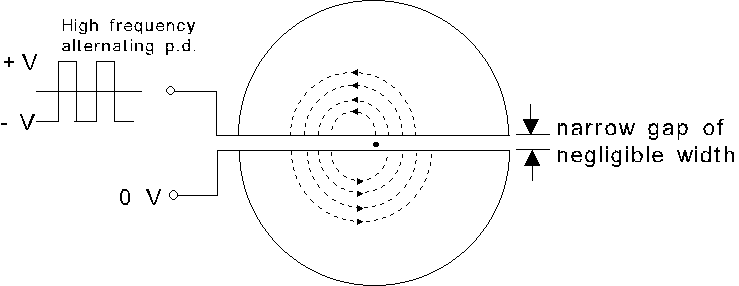
(c) Figure 9.1 shows the essential parts of a light-operated alarm circuit. The operational amplifier in the circuit acts as a voltage comparator so that the LED is on as soon as light is detected by the LDR. The resistance of the LDR drops from 100 kW to 10 kW in the presence of light.
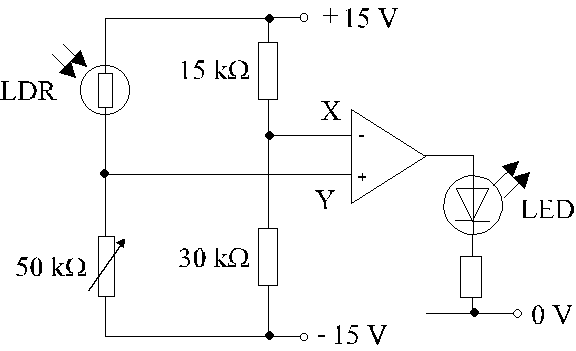
(I) Briefly explain the operation of the circuit. (3 marks )
(ii) State the minimum potential at Y for switching on the LED and calculate the minimum value of the resistance of the 50-kW rheostat below which the circuit will fail to operate. ( 3 marks )
10.
In an experiment to investigate the absorption of b and g rays by meterials, a source emitting b and g rays is placed at a distance of about 5 cm from a G-M tube as shown in
Figure 10.1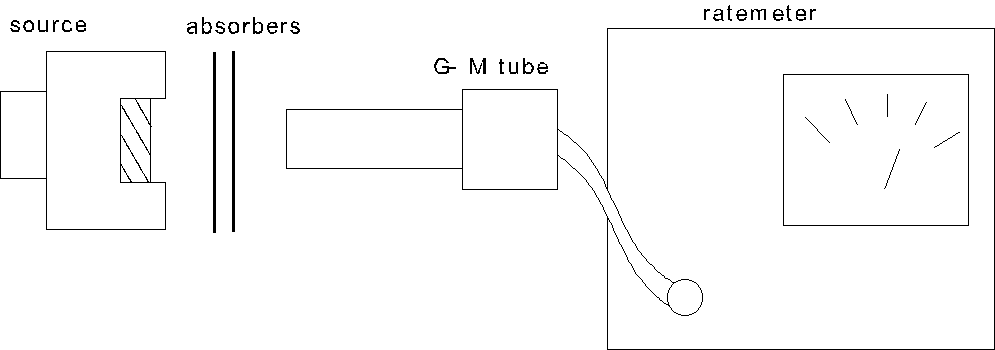
The count rates, N, are measured for different thickness, d, of absorber plates. The results shown in Figure10.2 with curve A corresponding to the measurements using aluminium absorber plates while curve B corresponds to those using lead absorber plates.
(a) (i) Curve A shows a considerable decrease in count rates up to a thickness of 7 mm; a further increase in d only results in a slight decrease in count rates. Explain why this
is so. (2 marks)
(ii) From the graphs in Figure 10.2, estimate the minimum thickness of lead needed to
absorb most of the b rays. (1 mark)
(iii) The source also emits a -particles. Explain why their effects can be neglected in this experiment. (1 mark)
(b) The count rates, N ', corrected for background, corresponding to different thicknesses, d, of lead absorber plates are tabulated as follows :
|
d/mm |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
N`/s-1 |
28.0 |
24.8 |
22.0 |
20.0 |
18.2 |
16.8 |
15.7 |
|
In N` |
(i) What is meant by the count rates being 'corrected for background' ? (1 mark)
(ii) Complete the table on the previous page and plot a graph of In N` against d.
(iii) Write down a relation between N` and d. ( 2 marks )