Problem Description
The stress at extreme fibers of a steel beam must be investigated in order to determine the probability of failure, the yield stress exceedence probability, and in order to verify the information given in Table 1 below. The stress is given by the following function: 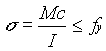 , where s = the calculated stress, c = the distance from the neutral axis to the extreme fibers, M = the applied moment on a section due to external loads, I = the centroidal moment of inertia of the cross section, and fy = the yield stress. Steel beams placed under a stress, s, greater than fy will fail.
, where s = the calculated stress, c = the distance from the neutral axis to the extreme fibers, M = the applied moment on a section due to external loads, I = the centroidal moment of inertia of the cross section, and fy = the yield stress. Steel beams placed under a stress, s, greater than fy will fail.
|
Table 1. Probabilistic Characteristics of c, M, I and fy. |
|
|
|
|
|
Random Variable |
Mean |
COV |
Distribution |
|
c |
10 |
0.05 |
normal |
|
M |
3000 |
0.30 |
lognormal |
|
I |
1000 |
0.08 |
normal |
|
fy |
50 |
0.15 |
lognormal |
Beams can fail in many different ways including bending, buckling, and shear forces. The beam might experience bending longitudinal stresses which cause failure when the steel is in tension or compression across its entire cross section. During bending, the beam might fail due to buckling (a rippling effect) if the compression flange is too thin. Excessive shear forces (sometimes near supports) might also cause the beam to fail. (Design of Steel 1999) When beams fail, damage and injuries may result. Steel beams are used in buildings and for other structural purposes and if the beam fails, buildings might collapse. Steel beams are also used in airplane design. If those beams fail, it might result in failure of the plane to function properly during take off and landing. Because of the dangers associated with beam failure, it is extremely important to research and analyze the stress at the extreme fibers of a steel beam.
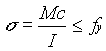 , where s = the calculated stress, c = the distance from the neutral axis to the extreme fibers, M = the applied moment on a section due to external loads, I = the centroidal moment of inertia of the cross section, and fy = the yield stress. Steel beams placed under a stress, s, greater than fy will fail.
, where s = the calculated stress, c = the distance from the neutral axis to the extreme fibers, M = the applied moment on a section due to external loads, I = the centroidal moment of inertia of the cross section, and fy = the yield stress. Steel beams placed under a stress, s, greater than fy will fail.