November: Various Equivalent Mean Theorems

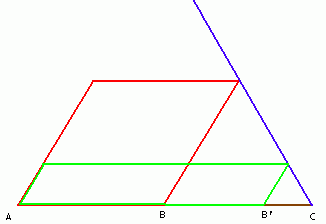
Well, it's november, and I here is the first of those neat things I wanted to celebrate on this page. It may look like a bunch of different theorems, but in fact they are all the same, only the language and "mindset" are different. The first version, and by far the oldest is the statement that in the diagram below

the green parallelogram never covers more area than the red one, where distance A to B is equal to the distance B to C. This version comes from greek geometry, and can be found in Euclid's Ellements

The second version, which looks like

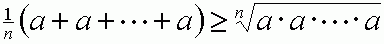
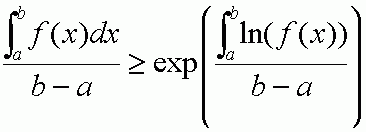
is due to Cauchy, and in english means that "the geometric mean of several numbers is never more than the arrithmetic mean those same numbers." Finally, an extension of the latter (which I found by myself, but may have been found by other people previously), and runs like this:

What I consider to be really clever about this is the exp(Integral(ln(F))). As a restriction in all of these one must say that the function or set of several numbers must always all be possitive, or else the geometric mean or ln(f) are not easily defined in a way useful to inequality math.

None of these theorems by themselves is reall terribly interesting, but as a set they are amazingly similar. This is where the beauty comes in.

translate the parallograms' sides and area into algebraic variables. the assertion reduces to the simplest case of (2). Next, let the function in (3) look like a bunch of steps, each 1 unit long in terms of x, and the height of each step is whatever you like(provided it's positive). again, the expression reduces to (2)! You can go the other way, and take the limit of (2) as n goes to infinity, and you will get (3). Again, Euclid's proof of (1) can be used as a model for the proof of the algebraic version, and this algebraic version is actually required for proving (2). Everything is the same!

any way, that's my theorem for this month. I will be setting up the proofs shortly.