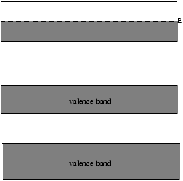
Figure 11.1 - A Metal



| Metals | Non-Metals |
| shiny and opaque | rarely reflects, sometimes transparent |
| all conduct electricity | resistivity varies up to a factor of 109 from sample to sample |
| conductivity falls as temperature rises | conductivity rises as temperature rises |
| obeys Ohm's Law | Sometimes obeys Ohm's Law |
| ductile | brittle |

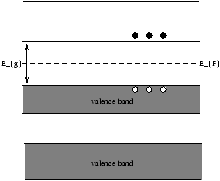
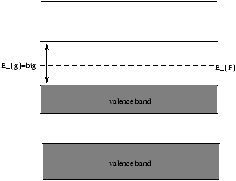
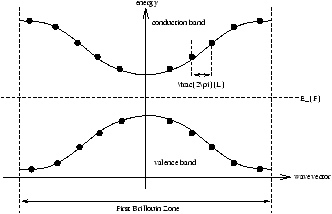
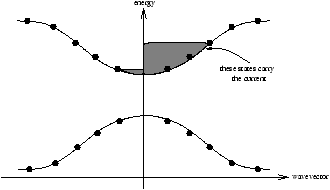
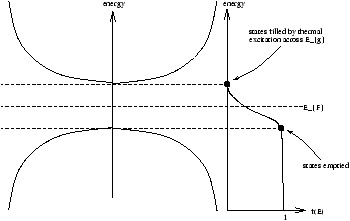
| niµ e |
|
| Ge | Si | GaA | Diamond | |
| Eg (eV) | 0.66 | 1.12 | 1.42 | ~ 4 |
| ni (cm-3 ) | 2e13 | 1.4e10 | 1.7e6 | almost zero |
| n= |
|
= |
|


