Controlo de fluxo e errosEstas são duas funções fundamentais para assegurar a ligação lógica. O controlo de fluxo é um mecanismo que evita que um nó receba mais dados do que pode absorver. O controlo de erros tem por missão corrigir erros na transmissão dos dados, o mecanismo mais usado é o ARQ ("Automatic Repeat Request"). Em ambos os casos os mecanismos usados envolvem retorno de informação de controlo do receptor para o emissor logo são fortemente afectados pelo atraso de propagação normalizado. Controlo de FluxoUm receptor usa um "buffer" finito tipo FIFO para armazenar temporariamente os dados até que os níveis superiores os absorvam (grosso modo trata-se de uma fila de espera), como o "buffer" é finito existe sempre alguma probabilidade de encher com consequente perda de dados.Para evitar esta situação o receptor tem de dar a conhecer ao emissor o estado do seu "buffer", o mecanismo mais simples de controlo de fluxo é conhecido por "stop & wait":
Este procedimento é muito afectado pelo atraso de propagação  Animação em Java Script O tempo total necessário para o envio de um pacote é dado pela soma das seguintes parcelas: tempo de transmissão do pacote (Tt); atraso de propagação; tempo de processamento no receptor; tempo de transmissão do ACK; atraso de propagação; tempo de processamento no receptor. Ou seja: Ttot = Tt + Tprop + Tproc + Tack + Tprop + Tproc Normalmente os valores mais significativos são Tt e Tprop, num calculo aproximado podemos desprezar os restantes, sendo então: Ttot = Tt + 2 x Tprop A eficiência de utilização da linha de transmissão (U) é dada pela razão entre o tempo de transmissão de um pacote e
o tempo de ocupação do sistema que isso produz, ou seja: Usando o atraso de propagação normalizado temos então: U = 1 / (1 + 2a) As redes locais não são neste aspecto muito afectadas pelo atraso de transmissão, numa rede local os valores de a estão geralmente na gama 0,01 a 0,1 dando normalmente origem a eficiências entre 83% e 98%. Em ligações de longa distância este fenómeno torna-se mais pesado, o caso extremo são as ligações por satélite onde os valores de a podem atingir a ordem dos milhares, e a eficiência se situa muitas vezes abaixo dos 10%. Aparentemente os valores elevados no atraso de propagação poderiam ser compensados pela utilização de pacotes de maior dimensão, originando valores mais elevados de Tt, contudo existem diversas razões pelas quais isso não é conveniente:
Protocolo de Janela Deslizante ("Sliding Window Protocol")A solução consiste no envio e ACK de pacotes em conjunto, o emissor começa por enviar um número de pacotes w que designaremos de "tamanho da janela". O tamanho da janela é o número de pacotes que podem ser enviados sem qualquer ACK do receptor.O tamanho de janela é conhecido tanto pelo emissor como pelo receptor, até porque este último tem de reservar inicialmente um "buffer" com capacidade para w pacotes, com "stop & wait" apenas necessitava de reservar espaço para um pacote. Para garantir o funcionamento do mecanismo, tanto os pacotes como os ACK são númerados de 0 a w. Esta númeração evita que o receptor tenha de enviar ACK individuais para todos os pacotes. Compreende-se facilmente o funcionamento sabendo que a regra base é de que o número de pacotes que podem ser enviados sem ACK do receptor é w. Por exemplo: Se o receptor envia ACK-8 quer dizer que já retirou do "buffer" todos os pacotes até PAC-8, nesta situação o emissor fica a saber que pode manter sem ACK os w pacotes depois do PAC-8.  Animação em Java Script A eficiência deste método depende do facto de o ACK-0 chegar antes ou depois de o emissor enviar w pacotes (esgotar a janela). Esta questão só se põe numa linha "full-duplex", se a linha é "half-duplex", tal como na animação acima, só depois de os pacotes chegarem ao destino e a linha se encontrar livre é que o receptor pode enviar o ACK. Numa linha "half-duplex" a eficiência nunca será de 100%. Pelo contrário, numa linha "full-duplex", tal como se pode verificar no esquema seguinte, desde que o ACK-0 chegue ao emissor antes de este esgotar a janela a emissão de pacotes pode ser continua. A figura seguinte ilustra o funcionamento numa linha "full-duplex" com w=4 e uma eficiência de 100%: 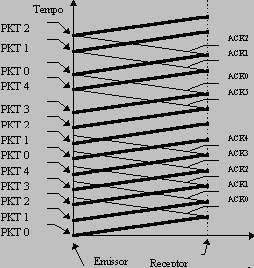 O tempo necessário a esgotar a janela é: w x Tt, normalizando (relativamente a Tt) será : w
Assim, se:
Os nós funcionam simultanemente como emissores e receptores, existindo circulação de pacotes e ACK nos dois sentidos, a técnica conhecida por "piggybacking" permite que os sinais de ACK sejam colocados nos pacotes que circulam em sentido inverso, aumentando a eficiência de utilização. O campo de "piggybacking" é implementado nos pacotes de dados e geralmente, mesmo que já tenha sido enviado um ACK individual, ele volta a ser enviado no pacote de dados pois é necessário preencher o campo e de qualquer modo este ACK funciona como um "backup" caso o primeiro se perca. O procedimento descrito explica a razão pela qual, para uma janela de w pacotes, existem w+1 números de sequência, imagine-se a seguinte situação numa linha "full-duplex":
Como os números de sequência são transmitidos na forma binária com n bits têm gamas com 2n valores distintos, enquanto a janela tem um comprimento w = 2n - 1. Mesmo sem "piggybacking", a utilização de w = 2n colocaria problemas sempre que ocorressem erros nos ACK:
Controlo de ErrosOs erros podem ser detectados recorrendo a diversas técnicas tais como o CRC, uma vez detectado o erro é necessário tomar providencias para o corrigir. A solução mais comum consiste na retransmissão do pacote danificado, este mecanismo é conhecido por ARQ ("Automatic Repeat Request")."stop & wait" ARQA implementação mais simples é o "stop & wait" ARQ que é em tudo semelhante ao esquema adoptado para o controlo de fluxo, a grande diferença é que a informação enviada ao emissor pode ser ACK ou NAK ("Negative Acknowledgment"):
Existe ainda uma situação a considerar: o pacote chega ao destino, mas o ACK ou NAK perde-se e não chega ao emissor, este volta a emitir o mesmo pacote que é aceite pelo receptor como se fosse um pacote novo. Para evitar esta situação tanto os pacotes como os ACK são numerados de 0 a 1. Tal como acontecia no controlo de fluxo o mecanismo "stop & wait" é fortemente afectado pelo atraso de propagação
normalizado: A solução é recorrer novamente ao protocolo de janela deslizante, a aplicação do protocolo de janela deslizante ao ARQ é conhecida por "ARQ continuo", existindo duas variantes: "go-back-any" e "selective-repeat". A técnica é absolutamente igual ao que foi descrito para o controlo de fluxo:
ARQ continuo "go-back-any"Quando é recebido um pacote com erro, é enviado um NAK ao emissor e todos os pacotes seguintes são ignorados até que o erro seja corrigido. Imagine-se uma situação em que w=7:
ARQ continuo "selective-repeat"O objectivo desta implementação é evitar que pacotes recebidos sem erros sejam retransmitidos. Retornando à situação anterior (w=7):
Numa implementação "go-back-any" não se levantam grandes problemas, o receptor ignora os pacotes 0 e 1, aceita os pacotes 2 a 6 e responde com ACK-6. Numa implementação "selective-repeat" tudo se complica porque os pacotes 3 a 6 foram recebidos sem erro e por isso o receptor fica disponível para aceitar o pacote 2 e os pacotes 7;0;1;2;3;4. Vai por isso aceitar correctamente o pacote 2, mas incorrectamente os pacotes 0 a 4 que vai colocar na janela seguinte, mas ainda pertencem à janela anterior. O problema é que como são aceites pacotes fora de sequência as retransmissões por "timeout" vão ser desastrosas. A solução é obrigar a que o tamanho da janela seja igual a metade da gama dos número de sequência, deste modo nunca é possivel que pacotes retransmitidos por "timeout" tenham números de sequência aceitaveis para o receptor: O "selective-repeat" é assim mais exigente quanto à largura da janela, nas implementações anteriores bastava w = 2n-1. Voltando novamente ao exemplo, para manter w=7 os números de sequencia terão de ser 0 a 13:
Numa implementação "selective-repeat" tudo fica agora claro, os pacotes 3 a 6 foram recebidos sem erro e por isso o receptor fica disponível para aceitar o pacote 2 e os pacotes 7;8;9;10;11;12. Vai por isso aceitar correctamente o pacote 2, e vai ignorar os restantes pacotes. O esquema seguinte ilustra o funcionamento do "go-back-any" e do "selective-repeat", com uma janela de 4 pacotes, numa linha "full-duplex", quando ocorre um erro na transmissão do pacote 2. 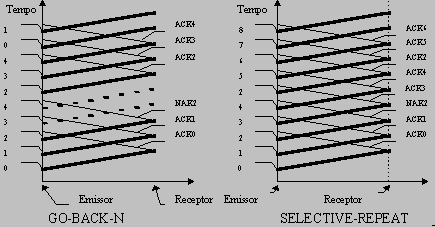 As duas linha a traço interrompido no esquema "go-back-any" correspondem a pacotes que são ignorados pelo receptor. Eficiência do ARQ "selective-repeat" e do ARQ "go-back-any"Tinhamos já visto que nos protocolos de janela deslizante a expressão geral da eficiência é:
Aplicando o mesmo raciocinio usado no "stop & wait" ARQ temos que o número de retransmissões médio de cada pacote é Nr = 1 / (1-p) , sendo p a probabilidade de ocorrencia de erro num pacote. O caso "selective-repeat" é em tudo semelhante ao "stop & wait": cada erro origina apenas uma retransmissão. Basta então dividir as expressões que ignoram os erros por Nr. Eficiência do "selective repeat":
Poderia obter-se que: Nr = (1 - p + kp) / (1- p) O valor de k depende da relação entre w e 2a + 1:
Eficiência do "go-back-any":
|