Criptografia

A encriptação ou cifragem consiste na aplicação de um algoritmo aos dados por forma a que eles se tornem ilegiveis, para recuperar os dados originais será necessario conhecer o algoritmo de desencriptação ou decifragem.

As aplicações básicas da criptografia são a confidencialidade (garantir que apenas quem autorizado pode ler os dados) e a autenticação/integridade (garantir que os dados têm a origem correcta e que não foram alterados entre origem e destino). Existem ainda outras aplicações, como por exemplo a assinatura digital.

Na prática, juntamente com os algoritmos utilizam-se chaves, mesmo que os algoritmos sejam conhecidos é necessária a chave correta.

A criptografia simétrica, também conhecida por criptografia tradicional utiliza uma única chave que serve tanto para cifrar como para decifrar. A criptografia de chave pública (mais recente) utiliza uma chave para cifrar e outra chave para decifrar.

Não existem mecanismos de cifragem/decifragem 100% eficazes, numa abordagem puramente teórica é imediato que qualquer chave pode ser quebrada pela força bruta (supondo que dispõe de um exemplar de uma mesma mensagem original e cifrada, e o algoritmo é conhecido, basta tentar com todas as chaves possíveis até acertar).

A solução é entrar no dominio prático e atender às capacidades do equipamento de processamento actual de modo a usar algoritmos e chaves que não possam ser descobertas em tempo útil. O tempo necessário para quebrar uma chave pela "força bruta" depende do número de chaves possiveis (número de bits da chave) e do tempo de execução do algoritmo.

O grande problema desta abordagem é que a capacidade de processamento dos equipamentos tem duplicado de 18 em 18 meses, logo de 18 em 18 meses é necessário aumentar um bit às chaves.

DES ("Data Encryption Standard")

O DES é um mecanismo de cifragem tradicional ("simétrico) desenvolvido nos anos setenta, utiliza uma chave de 56 bits que é aplicada a blocos de dados com 64 bits, o objectivo destes algoritmos é que seja muito dificil calcular a chave K, mesmo conhecendo o algoritmo DES, uma mensagem cifrada C e uma mensagem original M: C = DES(K,M)

O algoritmo usado é algo complexo:

  • A mensagem de 64 bits é dividida em duas partes de 32 bits cada.
  • A chave de 56 bits é usada para gerar 16 chaves de 18 bits cada.
  • É aplicado sucessivamente 16 vezes um algorimo, usando as chaves geradas.

Devido as suas caracteristicas pequenas alterações na mensagem original provocam grandes alterações na mensagem cifrada, isto dificulta as tentativas de conhecer a chave, mesmo que se possa cifrar aquilo que se pretende.

Note-se que as chaves DES têm 64 bits (8 octetos), mas o algoritmo obriga a que cada octeto da chave seja impar, logo o bit menos significativo da cada octeto não é usado porque tem valor fixo. Em termos reais temos por isso chaves com apenas 56 bits.

Embora seja dificil de implementar em "software" de uma forma eficiênte, foi desenvolvido "hardware" capaz de implementar este algoritmo de forma eficiênte.

A aplicação de "força bruta" para descobrir a chave, obriga a aplicar o algoritmo um máximo de 256 vezes, ou seja cerca de 72 000 000 000 000 000 vezes.

Este número não é contudo demasiado tranquilizante, este algoritmo é implementado de forma mais eficiente em "hardware", para "quebrar" uma chave DES usa-se um "chip" apropriado que pode ser montado de forma a trabalhar em paralelo com outros semelhantes. O custo depende do tempo em que se pretende quebrar a chave, em 1993 por 1 milhão de dolares podia-se montar uma máquina capaz de descobrir chaves DES em 3 horas e meia. O documento "Efficient DES key search" contém planos detalhados para a implementação desse tipo de máquina.

Para fortalecer o DES seria necessário aumentar o número de bits da chave, contudo o algoritmo exige um valor fixo de 56 bits, a aplicação sucessiva de duas chaves não é solução pois apenas duplica o número de aplicações do algoritmo necessárias para quebrar a chave (técnica "meet-in-the middle"), corresponde por isso a aumentar apenas um bit.

O triplo DES utiliza duas chaves, mas o algoritmo é aplicado três vezes segundo a seguinte equação:
C = DES( K1 , DES-1( K2 , DES( K1 , M ) ) )
, onde DES-1( representa o algoritmo inverso (decifragem). O triplo DES corresponde à utilição de uma chave de 90 bits, tem ainda a vantagem de poder ser usado para DES simples, basta que K1=K2.

Além da "força bruta", existem outras abordagem para descobrir chaves:

Cripto-análise diferencial
para usar esta técnica é necessário que se possa cifrar as mensagens que se pretende, em função de alterações nessas mensagens e resultados na mensagem cifrada, no caso do DES simples é possivel reduzir as chaves a 247.
Cripto-análise linear
tenta definir a chave por aproximação linear em função da informação recolhida de pares (M,C), no caso do DES simples reduz o número de chaves a 243.

Rivest Ciphers (RC2; RC4 e RC5)

Esta é uma sucessão de algorimos bastante usados na actualidade que possuem maior flexibilidade e possibilitam maior segurança do que o DES simples. Todos são algoritmos simétricos (a mesma chave é usada para cifrar e para decifrar).

Rivest Cipher 2 (RC2)

O RC2 caracteriza-se por blocos de entrada de 64 bits (8 bytes), contudo podem ser usadas chaves com vários tamanhos, o tamanho mais comum, por ser considerado seguro é de 128 bits (16 bytes).

Rivest Cipher 4 (RC4)

O RC4 não é uma técnica de blocos, trabalha em continuo com um fluxo de entrada de bytes e saída de bytes cifrados ou decifrados conforme o caso. Esta é uma técnica actualmente muito usada, por um lado porque funciona em fluxo continuo e por outro lado porque é bastante rápida (cerca de 4 vezes mais rápida do que o DES simples). Tal como o RC2 permite qualquer comprimento de chave, usando-se normalmente 16 bytes (128 bits).

Rivest Cipher 5 (RC5)

Esta é novamente uma técnica de cifragem em bloco, o RC5 caracteriza-se por uma grande flexibilidade e possibilidade de parâmetrização. Com o RC5 os blocos de entrada podem ter qualquer dimensão pré-determinada, a chava também pode ter qualquer comprimento, e também se pode pre-determinar o número de iterações do algoritmo.

O RC5 é como se pode deduzir muito flexivel, estando sujeito a uma serie de parâmetros que devem ser ajustados às necessidades particulares de cada caso. A mensagem original é fornecida ao algoritmo sob a forma de dois blocos de w bits, correspondendo ao alinhamento mais conveniente para o sistema em causa, os valores tipicos para w são: 16, 32 e 64. A mensagem cifrada possui forma idêntica.

Outro parâmetro importante é o número de aplicações do algoritmo (r), pode variar de 1 a 255. Para aplicar r vezes o algoritmo, vai ser gerada apartir da chave uma tabela com t = 2.(r+1) blocos de w bits.

A chave é especificada pelos parâmetros b e k, b especifica o número de bytes (octetos) que constitui a chave e k é a chave propriamente dita.

É habitual usar a notação RC5-w/r/b para especificar uma implementação particular RC5. Podemos dizer que o RC5-32/16/7 é equivalente ao DES. Os valores mais usados são RC5-32/12/16 e RC5-32/16/8.

O documento "The RC5 Encryption Algorithm" contém grandes detalhes sobre o RC5, incluido uma implementação em C.

International Data Encryption Algorithm (IDEA)

É mais uma técnica de cifragem simétrica em bloco que é usada na actualidade. Usa blocos fixos com 64 bits (8 bytes) e usa chaves com 128 bits (16 bytes). Na actualidade é considerada segura, mas ao contrário dos algoritmos RC usa chaves de comprimento fixo que certamente vão comprometer o seu futuro.

BLOWFISH

É um algoritmo simétrico conhecido pela sua velocidade, sendo bastante mais rápido do que o RC2 e o IDEA. Usa blocos fixos com 64 bits (8 bytes), mas as chaves podem ter qualquer comprimento (128 bits é o mais corrente na actualidade).

ARCFOUR

É um algoritmo considerado equivalente ao RC4, tal como o RC4 não usa blocos de entrada mas sim um fluxo contínuo de bytes e as chaves podem ter comprimento variável, novamente 128 bits é o valor mais corrente na actualidade.

Aplicação das técnicas de cifragem em bloco

As técnicas de cifragem em bloco (Ex: DES, RC2, RC5, IDEA, ...) podem ser aplicadas de diversos modos a mensagens de comprimento diferente do tamanho de bloco.

A técnica mais simples é conhecida por ECB ("Electronic Code Book"), consiste em dividir a mensagem em blocos de tamanho adequado, cifrar os blocos em separado e concatenar os blocos cifrados na mesma ordem. O grande inconveniente desta técnica é que blocos de mensagem original idênticos vão produzir blocos cifrados idênticos, isso pode não ser desejável.

A técnica CBC ("Cipher Block Chaining") evita este inconveniente, realiza a operação xor entre o bloco a cifrar Mi e o bloco anteriormente cifrado Ci, só depois aplica o algoritmo de cifragem:

Ci = cifragem( chave, Mi xor C(i-1))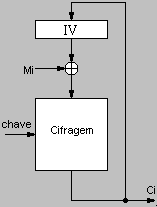

Na decifragem obtém-se Mi xor C(i-1), como xor-1 = xor, utiliza-se:

Mi = decifragem( chave, Ci) xor C(i-1)

Como para o primeiro bloco não existe mensagem anterior, utiliza-se um bloco aleatório conhecido por IV ("Initialization Vector").

Esta técnica é pouco favorável sob o ponto de vista da propagação de erros, uma vez que um erro na transmissão de um bloco cifrado Ci vai inutilizar tanto o bloco Mi como o seguinte M(i+1).

Nas técnicas CFB ("Cipher FeedBack") e OFB ("Output FeedBack") a mensagem não é directamente cifrada, existe um vector de inicial (IV) ao qual é aplicado o algoritmo de cifragem, aplica-se então a operação xor entre o vector cifrado e a mensagem.

A operação xor entre o vector cifrado e a mensagem é realizada do seguinte modo:

  • Pegam-se nos n bits da esquerda do vector cifrado e realiza-se a operação xor com os n seguintes da mensagem.
  • Realiza-se o "shift" para a esquerda de n bits do vector cifrado.
  • Injectam-se n bits no vector original, realizando o "shift" para a esquerda.
    • No caso do CFB utilizam-se os n bits resultantes da operação xor.
    • No caso do OFB utilizam-se os n bits retirados do vector cifrado.
  • Quando esgotam os bits do vector cifrado aplica-se novamente o algoritmo de cifragem ao vector original.

As figuras seguintes ilustram as duas técnicas: CFB (à esquerda) e OFB (à direita):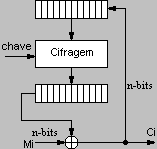

Os valores mais comuns para n são 1, 8 ou 64. Devido ao seu funcionamento a tecnica OFB, também conhecida por OFM ("Output Feedback Mode") apenas produz um bloco de mensagem errado quando ocorre um erro na transmissão de um bloco cifrado.

Quando o comprimento da mensagem não é multiplo do tamanho do bloco é necessário recorrer a técnicas de enchimento ("padding"), uma técnica habitual é adicionar um bit 1 seguido dos bits 0 necessários.

Distribuição de chaves

As cifragens simétricas em que básicamente a decifragem é o inverso da cifragem, usa-se a mesma chave na cifragem e decifragem que por razões obvias deve ser secreta, isto é apenas do conhecimento da entidade de origem e entidade de destino.

O grande problema levantado pela criptografia de chave secreta é a distribuição de chaves, poderiam ser enviadas por um sistema paralelo como correio ou "fax", mas o mais conveniente seria usar a rede de comunicação, para tal a chave deveria ser cifrada usando uma chave anterior.

Para estabelecer uma comunicação segura entre uma aplicação cliente e uma aplicação servidora, o ideal seria que o servidor e o cliente trocassem entre sí as chaves na altura do estabelecimento da conexão.

Para se conseguir uma situação deste tipo existem duas soluções:

  • Manter a criptografia de chave secreta e usar uma técnica especial para enviar a chave, por exemplo "puzzles".
  • Utilizar criptografia de chave pública que veio alterar radicalmente o modo de ver a criptografia.

"Puzzles"

Para fornecer a chave secreta é enviado um conjunto de "puzzles", geralmente na ordem das dezenas de milhar. Tomando o exemplo DES, cada "puzzle" é constituido por 120 bits zero, seguido do número do "puzzle" com 16 bits e finalmente uma chave, DES de 56 bits. Todos os "puzzles" são cifrados com chaves DES em que os últimos 22 bits são zero.

O cliente escolhe um "puzzle" à sorte e quebra a cifra usando força bruta, tem de tentar "apenas" 234 chaves, quando obtém 120 zeros no inicio sabe que consegui decifrar o "puzzle" e portanto possiu já a chave DES que escolheu (últimos 56 bits do "puzzle" decifrado). Tem agora de indicar qual o "puzzle" que escolheu, envia então uma mensagem com o número do "puzzle" cifrado com a chave DES escolhida, destinatário (ex.:servidor) conhece as chaves que iam nos "puzzles" e o respectivo número de "puzzle" e pode facilmente descobrir qual foi a chave escolhida.

O tempo médio que um intruso necessita para descobrir a chave situa-se na ordem dos anos e pode ser ajustado por variação do número de "puzzles" em jogo.

Definição de chave durante a autenticação

Num contexto mais restrito em que se utiliza autenticação por "password" protegida, esta autenticação pode ser usada para definir a chave secreta sem que seja transmitida pela rede. Este mecanismo tem contudo outras limitações.

Criptografia de chave pública

A criptografia de chave pública foi uma descoberta de enorme importância, consegui-se desenvolver algoritmos em que se usa uma dada chave para cifrar os dados, mas que não serve para decifrar, para tal é necessária uma segunda chave diferente da primeira. Por esta razão este tipo de algoritmos é designado por assimétrico.

Tipicamente a chave de cifragem é pública (é divulgada a todos os utilizadores), a chave de decifragem é secreta, normalmente usa-se aqui a expressão privada, para não criar confusões com a criptografia simétrica. Quando uma entidade A pretende enviar à entidade B uma mensagem cifra-a com a chave pública de B antes do envio. Ninguem, nem sequer a entidade A é capaz de decifrar, apenas a entidade B que possui a chave secreta adequada.

Além de resolver definitivamente o problema da distribuição de chaves, a criptografia de chave pública facilita significativamente a implementação de mecanismos de autenticação de mensagens e assinatura digital. Embora tenham sido propostos outros algoritmos, actualmente o RSA é o mais sólido, o algoritmo "Merkle-Hellman Knapsacks" demorou quatro anos a ser quebrado por Adi Shamir, uma segunda versão, supostamente mais sólida, demorou dois anos a ser quebrada. Actualmente praticamente pode-se afirmar que o RSA é o algoritmo de chave pública.

RSA

Este algoritmo é devido a Ron Rivest, Adi Shamir e Len Adleman (RSA), baseina-se no seguinte: é simples arranjar dois números primos grandes, mas é muito complicado (moroso) factorizar o seu produto. O RSA tem aguentado todas as investidas dos cripto-analistas, contudo temos que atender ao facto de ser um problema matemático, existe sempre o risco de descoberta de uma técnica para resolver o problema de forma eficiênte.

Geração das chaves:

  • Escolhem-se dois número primos grandes a e b.
  • Calcula-se n = a x b.
  • Calcula-se ø(n) = (a-1) x (b-1).
  • Escolhe-se um número pequeno p que seja primo relativo de ø(n) e < ø(n), calcula-se s tal que (p x s) mod ø(n) = 1, onde mod é o operador "resto da divisão inteira" (aritmética modulo ø(n)).
  • (Dois números são primos relativos se o maior divisor comum é 1)
  • O par (n,p) constitui a chave pública, d é a chave secreta.

Aplicação:

  • Cifragem: C = Mp mod n
  • Decifragem: M = Cs mod n

, onde M e C são respectivamente a mensagem original e mensagem cifrada, ambas com valores possiveis de zero a n-1.

Uma propriedade interessante do RSA é a possibilidade de inversão das chaves, pode-se cifrar uma mensagem com a chave s, para decifrar será agora necessária a chave pública: utilizável para autenticação e assinatura digital.

Para efeitos de exemplificação tomem-se os números primos a=7 e b=17:
n = a x b = 119
ø(n) = (a-1) x (b-1) = 96
como primo relativo de ø(n) podemos escolher p=5
então para obter p x s mod 96 = 1, podemos usar s = 77
pois 5 x 77 = 385, 385 mod 96 = 1
A chave pública é (5;119) e a chave secreta é 77

Exemplos de aplicação:
Para evitar perdas de dados torna-se necessário aplicar a seguinte propriedade da aritmética modular:

(a x b) mod n = ((a mod n) x (b mod n)) mod n
Para cifrar o número 2 com a chave pública temos C = 25 mod 119 = 32 mod 119 = 32
Para decifrar utiliza-se M = 3277 mod 119
, para usar uma calculadora, sem perder dados podemos usar 11 parcelas:
((327 mod 119) x ... x (327 mod 119)) mod 119
, obtemos então 2511 mod 119, podemos agora aplicar ((511 mod 119) x (511 mod 119)) mod 119 , obtemos agora 452 mod 119 = 2

Também se pode cifrar o número 2 com a chave secreta temos C = 277 mod 119
, para usar uma calculadora, sem perder dados podemos usar 11 parcelas:
((27 mod 119) x ... x (27 mod 119)) mod 119 = 911 mod 119 = 32
Para decifrar utiliza-se M = 325 mod 119 = 2
Para cifrar o número 3 com a chave pública temos C = 35 mod 119 = 243 mod 119 = 5
Para decifrar utiliza-se M = 577 mod 119
, para usar uma calculadora, sem perder dados podemos usar 7 parcelas:
((511 mod 119) x ... x (511 mod 119)) mod 119
, obtemos então 457 mod 119 = 3
Como se pode verificar as operações a realizar na decifragem não são simples, especialemente se atendermos a que os números a e b devem ser grandes.

Para os valores 0 e 1 a messagem e o resultado da cifragem coincidem, contudo isto não é muito grave, os valores usados para n são muito elevados (na ordem de 10200), o tamanho mais comum para as mensagens a cifrar (M) é de 512 bits (que representa números até mais de 10154), para este número de bits não são vulgares os valores 0 e 1, de qualquer modo isto pode ser resolvido pela adição de duas unidades a M antes de entrar no algoritmo de cifragem e subtração de duas unidades depois de sair do algoritmo de decifragem.

Gerar chaves RSA não é uma operação simples, o primeiro problema é arranjar dois números primos a e b com uma ordem de grandeza de 10100, usar os algoritmos tradicionais de geração de números primos é impossivel, a solução é usar testes eliminatórios, estes testes permitem saber se um número não é primo, ou qual a probabilidade de ser primo, se um dado número depois de testado intensivamente não é eliminado será adoptado. A segunda questão prende-se com a determinação de um primo relativo de ø(n), p ou s e de seguida é necessário determinar outro número para verificar a relação (p x s) mod ø(n) = 1.

O algoritmo RSA serve de base a muitos sistemas de segurança actuais, tais como o PGP ("Pretty Good Privacy"), usado em correio electronico. A seu grande inconveniente é a lentidão já que terá de ter como suporte sistemas capazes de lidar com números muito grandes. Na maioria dos casos o RSA é usado para distribuír uma chave de criptografia simétrica, apenas no ínicio de sessão, durante a sessão os dados são cifrados com essa chave, usando criptografia convencional, muito mais rápida.

Sob o ponto de vista de cripto-análise e devido ao número de bits das chaves a aplicação de força bruta (tentar todas as chaves secretas possíveis) está totalmente excluida, o algoritmo é lento e os tamanhos de chave RSA mais usados são 512 bits e 1024 bits. A abordagem é tentar obter os dois factores primos de n. Contudo tal é extremamente complexo para a ordem de grandeza usada para n, o tempo necessário cresce exponencialmente com o valor de n. Novamente interessa referir que o RSA se baseia num problema Matemático, estando por isso sujeito a alguma solução brilhante de algum génio.

Por curiosidade apresenta-se a seguir uma chave publica RSA de 1024 bits: 

RSA Public Key: (1024 bit)
                Modulus (1024 bit):
                    00:f6:9c:64:49:18:7f:c7:47:db:07:b6:a3:43:2e:
                    ef:6c:7a:56:dd:8a:87:18:37:cb:af:70:ea:5b:33:
                    96:d8:fa:4c:46:c3:be:f4:0a:6f:e4:d0:31:82:17:
                    f9:c2:3d:d9:6d:c7:57:79:fe:98:d7:64:12:80:84:
                    44:89:cd:f9:66:43:d4:ea:d2:54:5b:89:85:23:ff:
                    18:70:87:7d:f5:37:33:0c:3d:30:53:45:51:e9:4d:
                    cf:b7:31:5a:c8:a1:a9:3b:80:92:58:8b:a6:0e:a9:
                    83:16:83:91:3a:3f:99:72:23:5f:8a:dc:a1:1e:34:
                    73:5f:10:a9:fa:f0:d9:d4:ad
                Exponent: 65537 (0x10001)

Distribuição de chaves públicas

Embora a criptografia de chave pública resolva o problema da distribuição de chaves existe ainda a questão do modo como as chaves públicas serão obtidas por quem delas necessita.

As chaves públicas destinam-se a ser divulgadas, mas esta divulgação deve ser realizada de tal modo que não possa ser forjada por terceiros, as consequências seriam obvias.

O correio electrónico ou sistemas de news não são de todo adequados, uma melhor solução será a sua colocação na página WWW pessoal.

Uma opção mais segura é definir uma autoridade de chaves públicas, quando A pretende enviar uma mensagem a B realiza as seguintes operações:

  • contacta a autoridade C enviando-lhe um pedido com etiqueta temporal
  • C responde enviando uma mensagem cifrada com a sua chave secreta (assim A sabe que a mensagem veio de C), onde consta chave pública de B e a mensagem original
  • Quando B recebe a primeira mensagem de A terá de realizar o mesmo procedimento para obter a chave de B e lhe poder responder.

Certificados de chave pública

Apesar de mais seguro a existencia de autoridades de chave pública coloca alguns problemas em termos de quantidade de comunicações necessárias, uma alternativa é a emissão de "certificados de chave pública". Cada entidade contacta a autoridade de chave pública que lhe fornece um certificado contendo: uma etiqueta temporal; a identificação da entidade; a chave pública da entidade. O certificado encontra-se cifrado com a chave secreta da autoridade, este facto atesta a sua origem. As diversas entidades podem agora trocar directamente entre si estes certificados, o facto de estarem cifrados pela autoridade atesta a sua veracidade.

O texto seguinte apresenta o conteudo de um certificado de chave pública de 512 bits: 

Certificate:
    Data:
        Version: 3 (0x2)
        Serial Number: 0 (0x0)
        Signature Algorithm: md5WithRSAEncryption
        Issuer: C=PT, ST=PORTO, L=PORTO, O=dei.isep.ipp.pt, OU=DEI, CN=linuxbox
        Validity
            Not Before: Dec 27 17:17:44 2001 GMT
            Not After : Dec 27 17:17:44 2002 GMT
        Subject: C=PT, ST=PORTO, L=PORTO, O=dei.isep.ipp.pt, OU=DEI, CN=linuxbox
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
            RSA Public Key: (512 bit)
                Modulus (512 bit):
                    00:eb:cc:ba:1b:60:22:0b:2e:ac:35:7c:96:b0:2b:
                    34:ea:9d:fa:cb:92:5c:be:16:69:69:f7:32:31:d4:
                    77:cf:e8:25:76:ae:d3:0d:98:1f:91:4d:7d:4e:44:
                    84:4b:fd:13:4f:a4:1a:d0:6b:75:c6:12:21:93:4e:
                    42:5e:32:e6:c9
                Exponent: 65537 (0x10001)
        X509v3 extensions:
            X509v3 Subject Key Identifier: 
                BF:38:C6:55:62:F0:31:60:50:14:5F:5D:9E:80:17:AB:6D:3B:6B:41
            X509v3 Authority Key Identifier: 
                keyid:BF:38:C6:55:62:F0:31:60:50:14:5F:5D:9E:80:17:AB:6D:3B:6B:41
                DirName:/C=PT/ST=PORTO/L=PORTO/O=dei.isep.ipp.pt/OU=DEI/CN=linuxbox
                serial:00

            X509v3 Basic Constraints: 
                CA:TRUE
    Signature Algorithm: md5WithRSAEncryption
        52:c8:67:3c:75:d8:2e:5b:95:c4:6c:57:81:7d:74:34:44:1c:
        98:c8:58:a9:6f:d8:ea:e9:ee:2b:cf:28:6f:60:2d:4e:55:d0:
        cf:39:7c:cc:b9:8b:8f:1f:aa:de:5d:fa:ae:31:62:02:8b:15:
        a7:92:da:38:c6:ee:95:93:7b:e3

Este certificado foi emitido pelo proprietário da chave, isto é não se recorreu a nenhuma autoridade de chave pública para validar o certificado, o emissor ("Issuer") é a mesma entidade que possui a chave ("Subject"). O que prova a autenticidade do certificado é a assinatura digital que se encontra no final, esta assinatura é realizada usando a chave privada, de tal modo que quem recebe fica a ter a certeza de que a chave publica constante no certificado pertence a quem emitiu o certificado. Para verificar a autenticidade basta calcular o hash code do certificado (no caso com MD5), aplicar a chave pública à assinatura e os dois resultados têm de coincidir.

Este tipo de certificado, assinado pelo próprio, pode colocar reservas quanto à origem. Ficamos a saber que quem o emitiu é o legito detentor da chave, contudo sem a intervenção de terceiros não temos a certeza da sua identificação. Sob o ponto de vista de utilização em rede a insegurança devida a esta ausencia de autenticação pode não ser muito grave para um utilizador. Por um lado é normalmente o utilizador que contacta o serviço e se existir confiançe em que está a contactar o serviço certo o problema não se coloca. Por outro lado o "software" cliente guarda os certificados que vai recebendo, qualquer alteração do certificado será notificada ao utilizador.

Distribuição de chaves secretas (criptografia simétrica)

A criptografia de chave pública pode ser usada para obviar um dos grandes problemas da criptografia tradicional: a distribuição de chaves secretas. A motivação é o facto de a criptografia tradicional ser substancialmente mais rápida nas operações de cifragem e decifragem, proporcionando assim débitos de dados mais elevados.

A utilização mais directa consistiria no seguinte:

  • A aplicação A envia à aplicação B uma mensagem com a chave publica da A.
  • A aplicação B gera uma chave secreta convencional (simétrica) e envia-a a A cifrada com a respectiva chave publica.
  • A aplicação A decifra a mensagem com a sua chave secreta e obtém a chave secreta convencional.

Este mecanismo pode ser contudo furado por uma entidade C com controlo sob as transmissões:

  • C captura a primeira mensagem de A e fica a conhecer a chave pública de A.
  • C envia para B uma cópia da mensagem de A, mas substitui a chave pública pela sua.
  • C captura a resposta de B e fica a conhecer a chave secreta convencional.
  • para que A não note nada C envia a A a resposta que recebeu de B, cifrada com a chave publica de A.
  • C passa então a actuar de modo passivo, limitando-se a decifrar a conversação entre A e B.

O problema pode ser resolvido se previamente for usado um mecanismo seguro de distribuíção de chaves publicas e forem tomadas diversas precauções quanto a confidencialidade e autenticação:

  • A envia a B uma mensagem com a sua identificação e um identificador de transação I1(número que identifica a transação em curso), cifrada com a chave pública de B.
  • B enviar a A uma mensagem com I1 e um novo identificador I2, cifrada com a chave pública de A.
  • A tem a certeza que a mensagem veio de B devido à presença de I1, envia então a B I2, cifrado com a chave pública de B.
  • A gera a chave secreta convencional, cifra-a com a sua chave secreta e de A, cifra-a com a chave pública de B, e envia-a a B.
  • B recebe a mensagem e decifra-a aplicando primeiro a sua chave secreta e de seguida a chave publica de A.