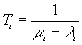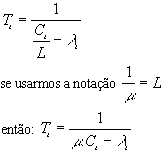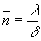Redes de Filas de Espera

Conhecimentos anteriores: Teoria de Filas de Espera

Uma das áreas da comunicação de dados onde a teoria das filas de espera é útil é no estudo do comportamento de redes de comutação:

Cada nó de uma rede comutada pode ser visto como um ou mais sistemas M/M/1. Para tal é necessário que o tempo entre chegadas de pacotes seja uma distribuição de Poisson.

Por outro lado e atendendo a que o serviço é a transmissão de um pacote através de uma linha, então o tempo médio de serviço é:

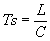, onde L é o comprimento dos pacotes em "bits" e C a capacidade da linha em bps. Como C é constante para uma dada linha, então se o comprimento dos pacotes for uma distribuição de Poisson então o tempo de serviço é ainda uma distribuição de Poisson.

Funcionamento de um nó de comutação

Um nó de comutação pode ser visto como um dispositivo com várias portas de entradas e saída de pacotes.

Quando chega um pacote o algoritmo de encaminhamento define a porta de destino.

Como existe possibilidade de a porta de destino estar ocupada é necessária uma fila de espera para cada saída. A figura seguinte representa um nó de comutação com 4 portas:

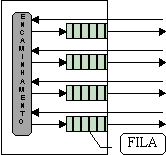O tempo de execução do algoritmo pode ser desprezado até porque geralmente o encaminhamento é realizado antes da recepção integral do pacote (o endereço de destino/caminho encontra-se definido no inicio do pacote).

As portas e as linhas entre nós devem ser "full- duplex", caso contrário seria necessário considerar os efeitos da introdução de mecanismos de controlo de acesso.

Uma vez que estamos a analisar as redes de comutação sob o ponto de vista de filas de espera, verificamos que a análise se deve centrar nas linhas e não nos nós.

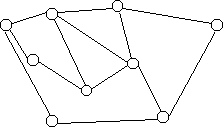
Redes de Filas M/M/1

Considerando uma rede com vários nós de comutação, verificamos que se trata de uma rede de filas de espera:

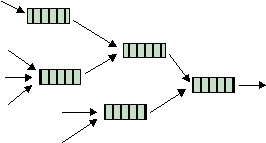Comparando com a primeira figura referente a uma rede de comutação verificamos que agora temos representações de tráfego de pacotes e que cada fila possui uma única saída.

Podemos observar que o processo de chegada de cada fila vai ser condicionado pelo processo de serviço da linha anterior (ou somatório dos processos de serviço, quando as linhas são várias) por esta razão continua a ter uma distribuição de Poisson (Burke, 1956).

Como o tempo de serviço depende do tamanho do pacote então o tempo entre chegadas vai depender também do tamanho do pacote. Deixa de haver independência entre a taxa de chegadas e o tamanho do pacote o que introduz correlações não aleatórias na rede.

Ignorando estas correlações está a supor-se que em cada nó os pacotes são redimensionados aleatoriamente (Poisson). Os resultados experimentais sustentam que esta aproximação é razoável.

Sendo Ts_i o tempo médio de serviço, em segundos, na linha i (tempo de transmissão de um pacote de comprimento médio), se o tamanho médio dos pacotes é de L bits e a taxa de transmissão nessa linha é C_i bits por segundo, então:

, sendo m_i a taxa média de serviço na linha i, em pacotes por segundo. Então o tempo total de atraso na linha i (T.F.E.) é dado por:

ou:

(este µ nada tem haver com a taxa de serviço, representa a fracção de pacote transportada por cada bit)

Onde Lambda_i representa a taxa média de chegadas à linha i (tráfego na linha i).

O tráfego total no interior de uma rede com t linhas é dado por:

Tráfego entre nós de entrada/saída

A rede é atravessada por pacotes que entram na rede por determinado nó e saem por outro nó. Em principio a rede não gera nem absorve tráfego.

Analisando os percursos seguidos pelos pacotes desde que entram até que saem da rede, podemos determinar vários parâmetros do funcionamento da rede no seu conjunto.

Representando por d_jk o tráfego externo (com origem e destino no exterior da rede) que entra pelo nó j e sai pelo nó k (pacotes/seg.), então, supondo uma rede com n nós, o tráfego externo total na rede é dado por:

Note-se que d_kj pode não existir para todos os nós, para os valores de k ou j correspondentes a nós intermédios d_kj=0 já que esse tipo de nó não se encontra em contacto directo com o exterior da rede.

Na maioria dos casos o tráfego externo é menor do que o tráfego interno, já que os pacotes ao descreverem um caminho j para k passam por várias linhas.

Quando a rede é constituída por uma única linha o tráfego externo é igual ao tráfego interno.

O número de linhas pelas quais um pacote passa é conhecido pelo número de "hops" (saltos entre nós).

O número de "hops" médio de um pacote numa rede é dado por:

Uma vez que Lambda_i/Lambda representa a probabilidade de um pacote passar pela linha i, então o atraso médio dos pacotes por linha é dado por: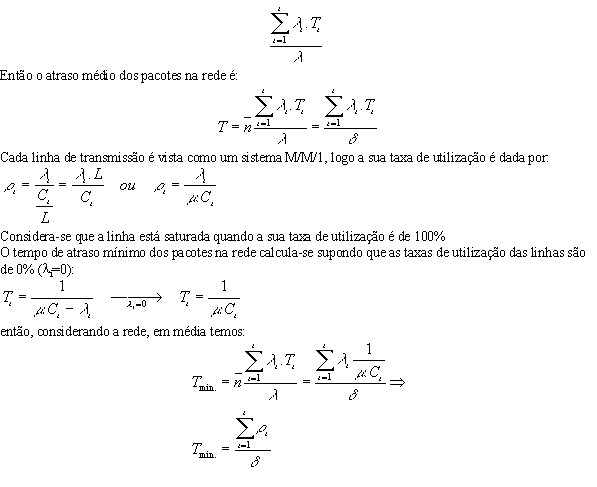