Image Processing

• Voroni Transform and Euclidean Distance Transform
• Deformable image registration
• Experiments

Distance transform is a useful tool in image processing, it can be used in mathematic morphology. Only Euclidean distance is translation and rotation invariant. However, most Euclidean distance transform algorithm can not reach linear time complexity. The first EDT algorithm of linear time complexity was reported in 1996, then I proposed another linear time algorithm which is even faster. Moreover, it general Voronoi diagram as a by-product without any more overhead.
The major features of the algorithm is summarized as below.
• Fastest Euclidean distance transform
• Compact data structure used in storing voronoi diagram
• The algorithm is published in paper
• Experimental results

Image registration is an essential task in most image analysis/understanding applications. Sometime, the type of the underlying transform is known a priori, such as rigid, affine, projective. Then, the problem of registration is reduced to be parameter estimation. However, in some cases the type of transform is unknown, or it can not be accurately described by any of the above transforms. How to register images with free-form deformation must be studied.
In our method we proposed a simplified elastic model and an iterative matching process. The simplified model derives a closed-form solution, and numerical method is no longer needed. Furthermore, a deliberately designed iteration control strategy guarantee both the accuracy and robustness of the method.
• Able to register images with any underlying tranform type (rigid, affine, projective, deformed)
• Robust and accurate
• The method is published in paper
• Experimental results

 

Fig 1 Voronoi diagram and Euclidean distance transform of 50 random dots

Fig 2 Euclidean distance transform of maple leaf contour
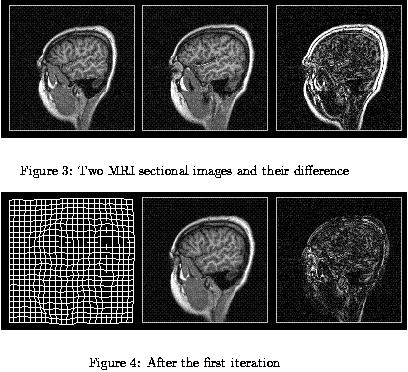