The Kicker
INTRODUCTION:
If, in a game of football, a place kicker kicks the ball with a given vertical and horizontal velocity from a given point on the field, we can use math to ascertain the trajectory of the ball. By determining the trajectory, we can find whether or not the ball will clear the goal post. Since we will not use Calculus in this problem, air resistance and wind speed will be neglected. We are given the following information that will help us determine the ball�s trajectory. The line of scrimmage is at the 43 yard line. The kicker will kick the ball from a point 7 yards behind the line of scrimmage. The goal post is 10 feet high and is at a point 10 yards behind the goal line. The kicker kicks the ball with a horizontal velocity of 50 feet per second and a vertical velocity of 60 feet per second. The acceleration due to gravity is the standard -32 feet per second squared.
The given information leads us in the direction of a few equations. Since we must first find when the ball will reach its maximum height, how high it will go, and when it will land, we will use an equation that gives us vertical height as a function of time. This vertical height equation is 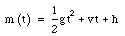 , where �g� is the acceleration due to gravity, �t� is time, �v� is vertical velocity, and �h� is the initial height. The quadratic formula will be needed in order to solve the problem, but we will only have to subtract, not add, the values in the numerator. Thus, the equation is
, where �g� is the acceleration due to gravity, �t� is time, �v� is vertical velocity, and �h� is the initial height. The quadratic formula will be needed in order to solve the problem, but we will only have to subtract, not add, the values in the numerator. Thus, the equation is 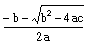 . We will also need to find the x-coordinate of the vertex, using the formula
. We will also need to find the x-coordinate of the vertex, using the formula 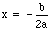 In order to find the horizontal distance, the simple formula of d=rt, where �d� is distance, �r� is rate, and �t� is time, will be necessary. By using those three formulas and some logical thinking, we can determine the trajectory of the ball.
In order to find the horizontal distance, the simple formula of d=rt, where �d� is distance, �r� is rate, and �t� is time, will be necessary. By using those three formulas and some logical thinking, we can determine the trajectory of the ball.
METHODOLOGY:
The first thing we need to know is when the ball will reach its maximum height. Since the aforementioned vertical height formula will be a parabola with the vertex indicating maximum height and the time of that height, we will use that equation. By substituting the given numbers into the equation, we create the equation 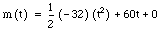 . After simplifying, we come up with
. After simplifying, we come up with 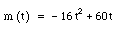 . Since the x-coordinate of the vertex indicates when the ball will reach its maximum height, we will find this using the equation
. Since the x-coordinate of the vertex indicates when the ball will reach its maximum height, we will find this using the equation 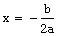 . By plugging in the numbers from the last equation, we find the x-coordinate of the vertex to be
. By plugging in the numbers from the last equation, we find the x-coordinate of the vertex to be 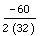 , simplified to 1.875. This is the amount of time in seconds that it will take for the ball to reach its maximum height. When we substitute this value for �t� in the vertical height equation, we derive
, simplified to 1.875. This is the amount of time in seconds that it will take for the ball to reach its maximum height. When we substitute this value for �t� in the vertical height equation, we derive 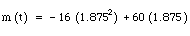 . After using simple arithmetic, we find that the maximum height is 56.25 feet. So we now know how high the ball will travel. But, in order to find out how far the ball will go horizontally, we need to know how long the ball will be in the air. We know that the time it takes for the ball to travel from the ground to the maximum height is equal to the time it will take for the ball to travel from the maximum height back to the ground. Therefore, we only have to double the time that we just found in order to find out how long the ball will be in the air. Thus, 2(1.875)=3.75 seconds.
. After using simple arithmetic, we find that the maximum height is 56.25 feet. So we now know how high the ball will travel. But, in order to find out how far the ball will go horizontally, we need to know how long the ball will be in the air. We know that the time it takes for the ball to travel from the ground to the maximum height is equal to the time it will take for the ball to travel from the maximum height back to the ground. Therefore, we only have to double the time that we just found in order to find out how long the ball will be in the air. Thus, 2(1.875)=3.75 seconds.
Now we need to find if the ball will reach the goal post. To find this, we use the linear equation d=rt. It was given that the horizontal velocity is 50 feet per second, and we found that the ball was in the air for 3.75 seconds. Plugging in 3.75 for �t� and 50 for �r� lets us find that the ball traveled 187.5 feet. So now we need to know where the ball will land. To find this, we use both the given information and the previous question. If the kicker is kicking the ball from a point 7 yards behind the line of scrimmage and the line of scrimmage is the 43 yard line, the kicker will be kicking from the 50 yard line. Because the goal post is 10 yards past the goal line, the kicker will be kicking from a point 60 yards away from the goal post. When we convert 60 yards into feet, we come up with 180 feet. Since the ball traveled 187.5 feet, the ball will land 7.5 feet beyond the goal post. Now we need to use the information we have found in order to see if the ball cleared the goal post. The goal post is 10 feet high, and the goal post is 180 feet away from the kicker, so in order to go over the goal post, the ball would have to be 10 feet high at the time that it had traveled 180 feet. So we need to find out when the ball will be 180 feet away from the kicker. We know the rate, 50 feet per second, and the distance, 180 feet, so we plug these two numbers into the formula d=rt, and we come up with 180=50t. When we solve for �t,� we find that the ball will be at the goal post after 3.6 seconds. The ball will at least make it to the goal post, but we still need to see if it will be more than 10 feet high at that point. To find out what height the ball will be when in reaches the goal post, we can use the vertical height formula, plugging in 3.6 for �t.� So we have the equation 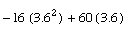 After simplifying we see that the ball will be 8.64 feet above the ground. Since 8.64 is less than 10, the ball will not clear the goal post.
After simplifying we see that the ball will be 8.64 feet above the ground. Since 8.64 is less than 10, the ball will not clear the goal post.
In order to plot the height of the ball versus time, we must use the vertical height formula. By using our original equation, 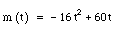 , and plugging in numbers, we come up with the following graph:
, and plugging in numbers, we come up with the following graph:
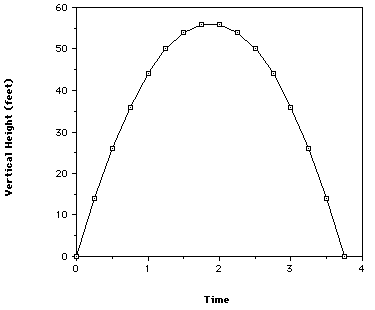
Note that the graph shows only the vertical distance, not the entire trajectory of the ball, since horizontal velocity is not taken into account. Now we need to plot the horizontal distance versus time. To do this, we use our equation of d=50t. By plugging in more numbers, we get the following graph:
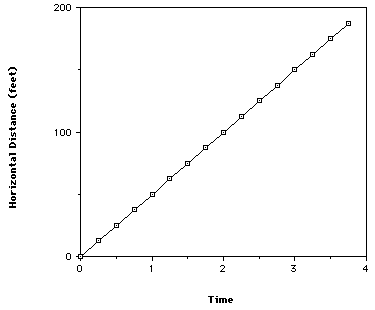
Finally, we need a horizontal distance versus time graph so that we know the ball�s trajectory. The vertical height will be on the y-axis since it is logical for vertical distance to be up and down, and for horizontal distance to be left and right. In order to create this graph, we must plug in the horizontal distances at a certain time interval as an x-coordinate, and plug in the vertical distance in that same time interval but as a y-coordinate. For example, at one second, the ball has traveled 50 feet. So we use that for one x-coordinate. At one second, the ball has also traveled 44 feet vertically. So that is our y-coordinate. So one plot is the point (50,44). We kept doing this for different time intervals so that we could have a graphical interpretation of the ball�s trajectory. This gave us the following graph:
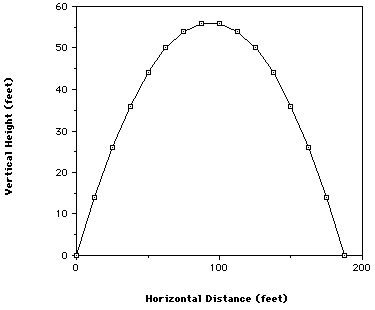
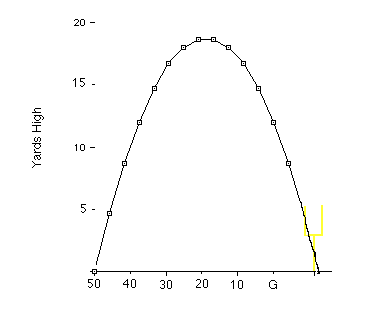
Now, we need to give a physical interpretation of the third graph. In order to do this, we need to first convert the distances from feet to yards. Then we need to replace the values of the horizontal distance with yard lines. In other words, we subtract the distance traveled from 50 and plot the new point on the football field. By doing this we get the following picture:
Now we need to know what the maximum line of scrimmage that the kick would be successful from. In order to find this, we use the vertical height formula again. However, this time we set the equation equal to 10 since we must know how long it took the ball to reach 10 feet when it came down. So, our new equation is 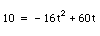 . Then, we move 10 over to the right side and we have a quadratic function. Since the equation cannot be easily factored, we will use the quadratic formula to find the answer. We want the largest answer since we want the time after it has gone down to 10 feet, not gone up to 10 feet. Thus, since the number inside the square root sign is going to be large and there is a negative number in the denominator, we will subtract the values on top rather than adding and subtracting them. This will yield the largest number. So, we get the equation
. Then, we move 10 over to the right side and we have a quadratic function. Since the equation cannot be easily factored, we will use the quadratic formula to find the answer. We want the largest answer since we want the time after it has gone down to 10 feet, not gone up to 10 feet. Thus, since the number inside the square root sign is going to be large and there is a negative number in the denominator, we will subtract the values on top rather than adding and subtracting them. This will yield the largest number. So, we get the equation 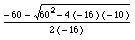 After simplifying, we get �t� equal to 3.575. That is how long it will take the ball to reach 10 yards in vertical height on its way down. Since the horizontal velocity is 50t, we will plug in 3.575 for �t� and have the horizontal distance that traveled when it hit 10 feet in vertical height. By plugging in the values, the horizontal distance is 59.586 yards. Thus, the kicker can be 59.586 yards away from the goal post and make a successful kick. Then, we will subtract 10 since the goal post is 10 yards beyond the goal line. So the point that the ball can be successfully kicked from is the 49.586 yard line. But the kicker is standing 7 yards behind the line of scrimmage. So to get the maximum line of scrimmage we subtract 7. Finally, the maximum line of scrimmage that will yield a successful kick is the 42.586 yard line.
After simplifying, we get �t� equal to 3.575. That is how long it will take the ball to reach 10 yards in vertical height on its way down. Since the horizontal velocity is 50t, we will plug in 3.575 for �t� and have the horizontal distance that traveled when it hit 10 feet in vertical height. By plugging in the values, the horizontal distance is 59.586 yards. Thus, the kicker can be 59.586 yards away from the goal post and make a successful kick. Then, we will subtract 10 since the goal post is 10 yards beyond the goal line. So the point that the ball can be successfully kicked from is the 49.586 yard line. But the kicker is standing 7 yards behind the line of scrimmage. So to get the maximum line of scrimmage we subtract 7. Finally, the maximum line of scrimmage that will yield a successful kick is the 42.586 yard line.
RESULTS:
In this problem, we found that the kicker could not, in fact, kick the ball over the goal post. By determining the horizontal and vertical distances at a certain time interval, we were able to see where the football was at at certain times. The first graph showed only the vertical height with respect to time. It did not necessarily indicate the ball�s trajectory, but in this particular problem that graph was very similar to the third one, which did show the ball�s flight path. The second graph was a simple linear equation, not a parabola, thus it could not indicate the path of the ball, only how far it traveled horizontally at certain time intervals. This graph would change if we would take air resistance and wind speed into account, but in this problem we assume that the horizontal velocity will not change. The third graph showed the football�s precise trajectory, showing the horizontal distance with respect to vertical distance. The physical interpretation showed us how that trajectory would look on a football field. It showed the yard lines rather than just numerical values in feet. That graph agreed with our equations that said although the ball would land past the goal post, it would still not clear the goal post.
DISCUSSION AND CONCLUSIONS:
In this problem, I used the quickest methods that were available by restricting myself to the formulas that were given by the math class that I was taking. Like any math problem, there was more than one way of finding the solution. There are formulas taught in physics and Calculus classes that can do the same things that I did, only some of them take wind speed and air resistance into account. Most of the work that I did was exact analysis, that is, not rounding numbers. It was only when the quadratic formula was used that I had to round and thus the answers may be slightly off after I used the quadratic formula. But that difference is minimal and has no effect on the answer. The results clearly showed that the ball would not go over the goal post.
If we used the technology that is available in other places, we could determine a kicker�s foot and leg strengths. Then we could see what the maximum velocities he could kick the ball at and determine his maximum range. Then, a football coach would not have to decide whether a 58-yard field goal was within his kicker�s range, he would know the range by mathematics. If we did that, we would have to take air resistance into account, since in a real life situation, there would be air on the football field. Then we would not be able to obtain accurate results with these equations. If, however, we wanted to determine how far a golf ball could travel on the moon, these equations would be valid, as long as we knew the vertical and horizontal distances. These equations, thus, are not limited solely to the mathematical realm, but they are also applicable to real life.
Back to the Main Essays page
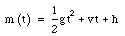 , where �g� is the acceleration due to gravity, �t� is time, �v� is vertical velocity, and �h� is the initial height. The quadratic formula will be needed in order to solve the problem, but we will only have to subtract, not add, the values in the numerator. Thus, the equation is
, where �g� is the acceleration due to gravity, �t� is time, �v� is vertical velocity, and �h� is the initial height. The quadratic formula will be needed in order to solve the problem, but we will only have to subtract, not add, the values in the numerator. Thus, the equation is 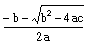 . We will also need to find the x-coordinate of the vertex, using the formula
. We will also need to find the x-coordinate of the vertex, using the formula 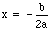 In order to find the horizontal distance, the simple formula of d=rt, where �d� is distance, �r� is rate, and �t� is time, will be necessary. By using those three formulas and some logical thinking, we can determine the trajectory of the ball.
In order to find the horizontal distance, the simple formula of d=rt, where �d� is distance, �r� is rate, and �t� is time, will be necessary. By using those three formulas and some logical thinking, we can determine the trajectory of the ball.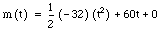 . After simplifying, we come up with
. After simplifying, we come up with 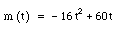 . Since the x-coordinate of the vertex indicates when the ball will reach its maximum height, we will find this using the equation
. Since the x-coordinate of the vertex indicates when the ball will reach its maximum height, we will find this using the equation 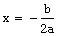 . By plugging in the numbers from the last equation, we find the x-coordinate of the vertex to be
. By plugging in the numbers from the last equation, we find the x-coordinate of the vertex to be 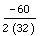 , simplified to 1.875. This is the amount of time in seconds that it will take for the ball to reach its maximum height. When we substitute this value for �t� in the vertical height equation, we derive
, simplified to 1.875. This is the amount of time in seconds that it will take for the ball to reach its maximum height. When we substitute this value for �t� in the vertical height equation, we derive 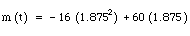 . After using simple arithmetic, we find that the maximum height is 56.25 feet. So we now know how high the ball will travel. But, in order to find out how far the ball will go horizontally, we need to know how long the ball will be in the air. We know that the time it takes for the ball to travel from the ground to the maximum height is equal to the time it will take for the ball to travel from the maximum height back to the ground. Therefore, we only have to double the time that we just found in order to find out how long the ball will be in the air. Thus, 2(1.875)=3.75 seconds.
. After using simple arithmetic, we find that the maximum height is 56.25 feet. So we now know how high the ball will travel. But, in order to find out how far the ball will go horizontally, we need to know how long the ball will be in the air. We know that the time it takes for the ball to travel from the ground to the maximum height is equal to the time it will take for the ball to travel from the maximum height back to the ground. Therefore, we only have to double the time that we just found in order to find out how long the ball will be in the air. Thus, 2(1.875)=3.75 seconds.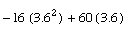 After simplifying we see that the ball will be 8.64 feet above the ground. Since 8.64 is less than 10, the ball will not clear the goal post.
After simplifying we see that the ball will be 8.64 feet above the ground. Since 8.64 is less than 10, the ball will not clear the goal post.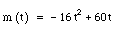 , and plugging in numbers, we come up with the following graph:
, and plugging in numbers, we come up with the following graph:



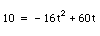 . Then, we move 10 over to the right side and we have a quadratic function. Since the equation cannot be easily factored, we will use the quadratic formula to find the answer. We want the largest answer since we want the time after it has gone down to 10 feet, not gone up to 10 feet. Thus, since the number inside the square root sign is going to be large and there is a negative number in the denominator, we will subtract the values on top rather than adding and subtracting them. This will yield the largest number. So, we get the equation
. Then, we move 10 over to the right side and we have a quadratic function. Since the equation cannot be easily factored, we will use the quadratic formula to find the answer. We want the largest answer since we want the time after it has gone down to 10 feet, not gone up to 10 feet. Thus, since the number inside the square root sign is going to be large and there is a negative number in the denominator, we will subtract the values on top rather than adding and subtracting them. This will yield the largest number. So, we get the equation 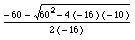 After simplifying, we get �t� equal to 3.575. That is how long it will take the ball to reach 10 yards in vertical height on its way down. Since the horizontal velocity is 50t, we will plug in 3.575 for �t� and have the horizontal distance that traveled when it hit 10 feet in vertical height. By plugging in the values, the horizontal distance is 59.586 yards. Thus, the kicker can be 59.586 yards away from the goal post and make a successful kick. Then, we will subtract 10 since the goal post is 10 yards beyond the goal line. So the point that the ball can be successfully kicked from is the 49.586 yard line. But the kicker is standing 7 yards behind the line of scrimmage. So to get the maximum line of scrimmage we subtract 7. Finally, the maximum line of scrimmage that will yield a successful kick is the 42.586 yard line.
After simplifying, we get �t� equal to 3.575. That is how long it will take the ball to reach 10 yards in vertical height on its way down. Since the horizontal velocity is 50t, we will plug in 3.575 for �t� and have the horizontal distance that traveled when it hit 10 feet in vertical height. By plugging in the values, the horizontal distance is 59.586 yards. Thus, the kicker can be 59.586 yards away from the goal post and make a successful kick. Then, we will subtract 10 since the goal post is 10 yards beyond the goal line. So the point that the ball can be successfully kicked from is the 49.586 yard line. But the kicker is standing 7 yards behind the line of scrimmage. So to get the maximum line of scrimmage we subtract 7. Finally, the maximum line of scrimmage that will yield a successful kick is the 42.586 yard line.