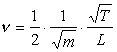
n
[Hz]
(frequency)
T [N] (tension)
m [kg/m] (linear mass)
L [m] (length of the vibrating part)
Acoustics Handbook
Dedicated to Brian May, guitarist of Queen
Alberto Orlandini
| Index | |
| The sound | The sound |
| Speed | Speed |
| Speed in the air in function of temperature | |
| Frequency | Frequency |
| Frequency of a sound generated by a string | |
| Music notes | Music notes |
| The natural scale | |
| The temperate scale | |
| Table of the frequencies of the music notes | |
| Wavelength | Wavelength |
| Doppler Effect | Doppler Effect for the sound |
| Doppler Effect for the light | |
| Intensity | Intensity |
| Sound pressure | |
| Sound power | |
| Levels and decibel | Levels and decibel |
| Sound pressure level | |
| Sound power level | |
| Credits | Credits |
A sound wave consists in slight variations of the atmospheric pressure which follow an harmonic law. In mathematical terms:
| p = patm + ps , where ps = p0�sin(2p n t) |
p [Pa]
(pressure) |
| ps is the sound pressure or relative pressure, and does vary in the time. | |
| patm is
the atmospheric pressure when there is silence, and it is a constant value much bigger than ps. |
|
The sound does not propagate in the vacuum because there is no pressure.
Speed [m/s]
Speed represents the distance
covered by the sound wave in one second.
The speed of sound depends on the medium of propagation and on the temperature.
It seems Isaac Newton was the first who measured the speed of sound in the air.
speed in the air at 20 �C
(i.e. 68 �F)
= 343 m/s
speed in the water at 20 �C (i.e. 68 �F) = 1525 m/s
speed in the iron = 5000 m/s
Speed in the air in function of temperature
The speed of sound in the air depends on the temperature and can be obtained using the following formula:
| v = 0,6 T + 331 [Centigrade temperature]
v = T/3 + 320 [Fahrenheit temperature] |
v [m/s]
(speed of sound in the air) T (temperature) |
Frequency [Hz = s-1]
Frequency
represents the number of oscillations the wave describes in one second.
The average human ear can perceive sounds whose frequency is between
40 Hz and 15000 Hz.
As to the emission, if we consider only the sole main frequency � the one proper of
the note emitted � excluding all the other harmonics, the human vocal range goes
from 70 Hz to 1000 Hz or more, that is from a D(1) to a C(5) or more.
Actually just a few human
beings can really cover such a wide range � it is almost 4 octaves!
On the basis of their frequency, sounds are classified in music notes.
Frequency of a sound generated by a string
The following formula was
hypothesized by Galileo Galilei and then turned out to be right.
It returns
the frequency of a sound generated by a vibrating string:
|
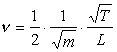n
[Hz]
(frequency) |
The vibration of the string produces also other sounds whose frequencies are multiples of that returned by the formula. These sounds are called harmonics.
Human beings distinguish sounds on the basis of their frequency, or better on the basis of the ratio of frequencies. The human ear has a logarithmical perception of frequency: more precisely, each octave corresponds to a doubling or a halving of frequency.
The problem of choosing a music
scale consists in the choosing of a succession of tones, called notes, with
opportune intervals, in order to allow a certain kind of music.
In particular it is very important to know what happens when two or more notes
are played together (functional harmony).
Since the times of Pythagoras it is known that two sounds played together provoke a pleasurable sensation only if the ratio of their frequencies is that of two small integers (1/2, 2/3, 3/4...). If so the sounds are called consonant. Else they are called dissonant.
The following table shows the more common consonant ratios in music:
| octave | 2/1 |
| fifth | 3/2 |
| fourth | 4/3 |
| third major | 5/4 |
| third minor | 6/5 |
| sixth major | 5/3 |
The natural scale is attributed to the Grecian philosopher Aristoxenus Tarentinus (500-400 B.C.) and consists in a succession of notes with increasing frequencies.
After fixing the frequency of the first note - the C of the scale -, the frequencies of the other notes are determined from the rations indicated in the following table. On the last C the following octave begins and the operation can be repeated.
| C | 1 |
| D | 9/8 |
| E | 5/4 |
| F | 4/3 |
| G | 3/2 |
| A | 5/3 |
| B | 15/8 |
| C | 2 |
The ratio is referred to the frequency of the first note of the scale.
In the natural scale the ratio of the frequencies of two notes which differ for one tone is not always the same. Consequently a certain melody cannot be played starting from a random note of the scale. For instance, a melody starting with the two notes C and D (ratio 9/8) cannot be transposed one tone higher, since the ratio of the frequencies of E and of D is very near ((5/4)/(9/8) = 10/9), but not equal to 9/8.
To
obviate this inconveniency, we use the so-called temperate scale, which
constitutes the compromise adopted in the western music.
It is obtained by dividing one octave in twelve intervals, called semitones or
halfsteps, so that the ratio of the frequencies of two consecutives semitones is
constant and equal to 
=
1,059463
The following table allows a comparison between the natural scale and the temperate scale:
|
Note |
Temperate Scale | Natural Scale | |||
| Exponent | Power | Value | Fraction | Value | |
| C | 0 | 20/12 | 1,000 | 1/1 | 1,000 |
| C# / Db | 1 | 21/12 | 1,059 | ||
| D | 2 | 22/12 | 1,122 | 9/8 | 1,125 |
| D # / Eb | 3 | 23/12 | 1,189 | ||
| E | 4 | 24/12 | 1,260 | 5/4 | 1,250 |
| F | 5 | 25/12 | 1,335 | 4/3 | 1,333 |
| F# / Gb | 6 | 26/12 | 1,414 | ||
| G | 7 | 27/12 | 1,498 | 3/2 | 1,500 |
| G# / Ab | 8 | 28/12 | 1,587 | ||
| A | 9 | 29/12 | 1,682 | 5/3 | 1,666 |
| A# / Bb | 10 | 210/12 | 1,782 | ||
| B | 11 | 211/12 | 1,888 | 15/8 | 1,875 |
| C | 12 | 212/12 | 2,000 | 2/1 | 2,000 |
If we
look the values of the powers of
and the values of the fractions, it is amazing how much they are
similar. For music it is a luck that the difference between the two scales is
almost imperceptible. Which of the two scales is the righter?
Does the human ear perceive the fractions or the exponents of ?
A certain answer does not exist, but since the human ear cannot perceive any
difference between the two scales, it is not essential to find an answer.
The
value =
1,059463 is the same value which you would find if you calculated the ratio of
the widths of two consecutive frets of a guitar. The twelfth fret divides the
string in two exact halves. For more information see the section Programs
Table of the frequency of the music notes
Conventionally the note of
reference is the central A.
We know from flutes that during the Renaissance it was higher than 460 Hz.
In 1859 the French A was officially fixed at 435 Hz. This frequency was later
adopted as the international diapason normal in 1887 in Wien. Yet, the British A
was still fixed at 440 Hz.
Nowadays A is conventionally
fixed at 440 Hz everywhere.
There are different ways to
indicate the octaves. Usually 440 Hz is
the frequency of A(3), but sometimes it's possible to find that 440 Hz is called
A(4) or A(2). Here below 440 Hz is assumed to be
A(3).
|
|
|
|
The bass A on guitars (5th string) is 110 Hz
Wavelength [m]
The wavelength is the distance
between two consecutive points where the atmospheric pressure is minimal or
maximal.
Knowing speed and frequency, it is possible to obtain the wavelength with the
following formula:
| l = c / n | l
[m] (wavelength) |
The wavelength of the hearable sounds goes from inches to metres.
If the source or the receiver of a wave are moving, the speeds do not sum up with the proper speed of the wave in the medium. In fact, the speed of propagation of the wave in the middle does not vary. What varies is the frequency.
The following formulas will contain the following symbols:
| l | [m] | wavelength |
| n | [Hz] | frequency |
| c | [m/s] | proper speed of sound in the medium |
| v | [m/s] | speed
of the source or of the receiver respect to the medium positive if causes approach between source and receiver negative is causes removal between source and receiver |
Source in movement respect to the medium:
 |
 |
Receiver in movement respect to the medium:
 |
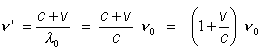When both source and receiver are in movement respect to the medium:
 |
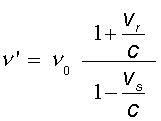vr = speed of the
receiver respect to the medium vs = speed of the source respect to the medium positive if
cause approach between source and receiver |
If also the medium is in
movement (for instance, if the wind is blowing), vr e vs
must always be expressed respect to the medium. Yet, in this case it may be more
comfortable to keep expressing vr e vs respect to the
ground, replacing c with:
c� = c + vm (where vm is the speed of the medium
respect to the ground).
Moreover, if the motion of the source or of the receiver are not on the same direction of the propagation of the sound, but in a direction inclined of an angle a, the fraction v/c has to be multiplied for cos(a)
The difference between the variations of frequency in the two cases (source in
movement, receiver in movement) is a real difference which can be perceived
experimentally.
This difference also as a notable theoretical importance, because it shows that
the two situations are really different.
| Doppler Effect for sound waves |
| The relative motion
between source and receiver does not count. What counts are the absolute motions of both respect to the medium. |
For the electromagnetic waves and for the light, which propagate also in the vacuum, the medium does not count any longer. Instead, what counts is the relative motion between source and receiver.
With the opportune relativistic Lorentz's corrections we have:
 |
v = relative speed between
source and receiver
positive if they approach |
For small values of v/c , the formula above can be approximated with one of the two expressions we had found for the sound waves.
In fact, for x tending to
zero: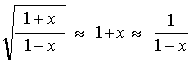 
If the speed of the source is
bigger that the speed of the wave in the medium:
- for the light it is not possible
- for the sound, there will be no waves before the source;
in this case the waves accumulate behind the source and form a shock wave
which is heard as a sonic boom (supersonic aircraft)
The sound intensity is commonly called volume.
Sound pressure [Pa = N/m2]
The sound pressure represents the force exerted by the sound wave on one m2 of surface.
The eardrum is always subject to the atmospheric pressure, which is more or less constant. In presence of a sound or of a noise, the eardrum is also subject to the pressure exerted by the sound wave, which sums up to the atmospheric pressure. Remember that, indicating with ps the sound pressure, the total pressure exerted on the eardrum is given by:
p = patm + ps , dove ps = p0�sin(2p n t)
The bigger is the difference of pressure between the points where the pressure is maximal and the point where the pressure is minimal, the higher is the volume perceived.
The sound pressure is always
relative to the listener
and it is inversely proportional to the distance from the source.
Sound power [W]
The sound power represents the acoustic energy emitted by a source in one second.
The instantaneous power is
generally much smaller than the maximal power
(For instance: a speaker whose label declares a maximal nominal power of 50
W, will hardly reach that power. The instantaneous power will usually stay
around 1 W)
The sound power is always relative to the sole source.
Levels [dB]
The logarithm of the ratio of a
given quantity and a constant quantity of reference is called level.
Of course the two quantity must be of the same kind and must be expressed with
the same unit of measurement.
The unit of measurement of the sound levels is the decibel, whose symbol is dB.
The instrument of measurement is the phonometer.
It is relative to the listener and depends of the distance from the source
Lp = 10 Log10 [ ( p / p0 )2 ] = 20 Log10 [ ( p / p0 ) ]
p0 is the sound pressure of reference, which is conventionally fixed at 20 �10-6 Pa
It is relative to the sole source, and does not depend on the distance
Lw = 10 Log10 ( W / W0 ) = 10 Log10 W + 120 dB
where W is the instantaneous
power of the source expressed in watt
[W]
W0 is the sound power of reference, which is conventionally fixed at 10-12 W
Sound pressure level in function of the distance from the source
The sound pressure is inversely proportional to the distance from the source
LB � LA = � 20 Log10 ( rB / rA )
DL
= � 6 dB
every time the distance is doubled
DL
= � 20 dB
every time the distance is increased 10 times.
Sound pressure level in function
of the distance of the source
when the sound power level is known
Lp = Lw � 20 Log10 ( r ) � 10
where r is the distance from the source expressed in metres.
Some formulas and definitions are taken from
books, common knowledge and other sources.
Several parts, especially the parts about music notes and acoustics, have been
written by Alberto Orlandini himself.
The exposition of all the topics as well as the organization of the exposition
is by Alberto Orlandini.