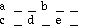4. A
short glance at the theoretical model
4.1 Variables
and terminal symbols
A
terminal
symbol
is a symbol to which a single
sound-object
may
be assigned. Terminal symbols are either predefined (see QuickStart §1.4:
simple
notes)
or enlisted in an
alphabet
file
(with prefix "-ho.").
Terminal
symbols always start with a lower-case character a..z, or a character in the set
ÄÅÇÉÑÖÜáàâäãåçéèêëíìîïñóòôöõúùûüAEaeøÀÃÕOEoeÿßØμ∂ΣΠπΩƒΔ¥#•
and
may contain any character in the above set or in the additional set:
0123456789#%*@¢£§◊$®©®\'"†°´´¨≠∞±≤≥ªº¿¡√“”""''÷
These
restrictions are not applicable to terminal symbols defined between single
quotes in a grammar.
Terminal symbols may be mapped to one another through one or several
(non-erasing)
homomorphisms.
A homomorphism named 'OCT' may for instance be used to define octaves in a
terminal alphabet of simple notes in the English convention:
OCT
C0
--> C1 --> C2 --> C3 --> C4 --> C5 --> C6 --> C7 --> C8
--> C9 --> C10
C#0
--> C#1 --> C#2 --> C#3 --> C#4 --> C#5 --> C#6 --> C#7
--> C#8 --> C#9 --> C#10
Db0
--> Db1 --> Db2 --> Db3 --> Db4 --> Db5 --> Db6 --> Db7
--> Db8 --> Db9 --> Db10
D0
--> D1 --> D2 --> D3 --> D4 --> D5 --> D6 --> D7 --> D8
--> D9 --> D10
D#0
--> D#1 --> D#2 --> D#3 --> D#4 --> D#5 --> D#6 --> D#7
--> D#8 --> D#9 --> D#10
etc...
Similarly,
a homomorphism named 'TRANS' would for instance transpose all simple notes one
semitone higher:
TRANS
C0
--> C#0 --> D0 --> D#0 --> ...
These
homomorphisms are edited in the "Alphabet" window
and stored in "-ho.<name>"
files. See for instance "-gr.MyMelody", §4.10 infra. Examples of
homomorphisms doing tonal transformations
other than transpositions may be found in "-gr.Ruwet"
and in "-gr.cloches1".
A
variable
is a symbol bound to be rewritten as a string of terminals and/or variables (in
a
derivation
of the grammar). The label of a variable is either an alphanumeric string
starting with an uppercase character, or written between |vertical bars|, and
may otherwise contain any character in the set:
ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz\-_#@*%$"%'•
When
BP2 reads a grammar it first assumes any unknown word to be a variable.
Therefore, if that word is not between vertical bars and does not begin with an
uppercase character, an error message is returned. Be careful to separate
variables with spaces or tabulations. If you write "XYZ", a variable named
"XYZ" is created although you perhaps meant "X", "Y" and "Z"... However,
spacing is not necessary for stringing together predefined tokens like terminal
symbols.
The
concepts of terminal symbols
and variables
are slightly different in BP grammars and conventional formal grammars. In
formal grammars, "terminals" are the symbols that cannot be rewritten; in BP
grammars they denote labels of hypothetic sound-objects. BP2 makes no
difference between terminal symbols and variables as far as derivations are
concerned. This means that even BP terminal symbols might be used as variables
in production rules. (Not recommended)
4.2 Starting
symbol
A
rewriting system operates transformations on strings of symbols. In formal
grammars, a special symbol is used to indicate the initial work string (the
starting
symbol).
This initial symbol is generally notated 'S'. It is also the default one
assumed by BP2. You may nevertheless wish to use a different symbol, or even a
string of variables as a start string.
See QuickStart §3.9.
4.3 Patterns
in BP grammars
A
pattern
is a string of terminals and variables derived in a particular way: the
derivation is obtained by replacing every variable with another pattern. For
instance, if {a,b,c,...z} is a terminal alphabet, pattern "XfYXXY" may be
derived as "abfYababY", "XfaZccXXaZcc", "abfaZccababaZcc", "abfaedccababaedcc",
etc. using the following derivations:
X
=> ab , Y => aZcc , Z => ed
The
set of all possible
terminal
derivations
(e.g. "abfaedccababaedcc") of a pattern is called the
language
generated by this pattern. A
pattern
language
is infinite unless some rules are used to define a limited number of acceptable
derivations.
A
grammar containing patterns may be called a
pattern
grammar.
See for instance §4.5.
4.4 BP2
grammars
The
language generated by a BP2 grammar is the intersection of a pattern language
and an unrestricted (phrase-structure or type 0) language (Salomaa 1973:15,
Révész 1985:6, Bel 1989). A
production
rule
is written
P
--> Q
in
which "P" (the
left
argument)
and "Q" (the
right
argument)
are strings of variables and/or terminals; the left argument should contain at
least one variable.
The
right argument may be the
empty
string.
In formal language literature the empty string is often notated '
l',
for instance:
S
-->
l
Since
'
l'
is not accessible on the keyboard you may type any of the following:
S
-->
S
--> lambda
S
--> nil
S
--> empty
S
--> null
Reserved
tokens 'lambda"', 'nil', 'empty' and 'null' may not be redefined as terminal
symbols.
In
derivations of a formal grammar, a string containing several occurrences of a
single variable is normally not handled as a pattern: each occurrence may be
derived independently. Therefore a special format is needed for patterns. If
for instance "YabZXcYXdX" is a pattern, it is necessary to indicate explicitly
that all occurrences of "X" (resp. "Y") must be derived identically. The
notation used in BP2 grammars is
(=Y)
abZ (=X) c (:Y) (:X) d (:X)
in
which brackets flagged with '=' are
reference
expressions
and brackets with ':'
slave
expressions.
Multilevel bracketing
is possible. For instance, the following BP2 grammar
S
--> (= (= X) S (:X)) (: (= X) S (:X))
S
--> nil
X
--> a
X
--> a S b
X
--> b
generates
self-similar fractals.
Bracketing
is also used to indicate homomorphic transformations.
For instance, given the TRANS and OCT homomorphisms (see §4.1 supra),
pattern
TRANS
TRANS (=X) (:X) OCT TRANS TRANS TRANS TRANS (:X)
would
represent three occurrences of the same structure of simple notes "X", the
first one being two semitones higher, and the last one four semitones and one
octave higher than the second one.
Brackets
and other structural markers are removed once a terminal string (a
sentence
or
item)
has been generated.
BP
grammars are generally arranged in several layers of
subgrammars
separated with lines of hyphens. These may be called
transformational
grammars
(in a non-linguistic sense, see Kain 1981:24-5). Each
subgrammar
may have its own
derivation
mode:
--
"RND"
mode: rules are applied in a random order. (Default mode)
--
"LIN"
mode: candidate rule chosen randomly among rules yielding a leftmost derivation.
--
"ORD"
mode: candidate rules are applied in the order in which they appear in the
grammar.
--
"SUB"
mode: same as "RND", but all occurrences of the selected rule's left argument
in the work string are rewritten simultaneously. In this mode, for instance,
p-substitutions
and other kinds of automatic (infinite) sequences may be generated. (See
§4.14 infra.) These derivations stop either when a predefined buffer
length has been reached, or the weights of all candidate rules are null as the
result of having been dynamically decremented during computation, or by
clicking the mouse.
--
"SUB1"
mode: same as "SUB", but only one rewriting of variables will be allowed. This
mode is much faster than "SUB" and may be used when it is certain that the
first substitution yields only terminal symbols. (See example in "-gr.Mozart",
§5.4 of QuickStart)
Below
is an illustration of a "LIN" subgrammar ("-gr.tryLIN").
We need to produce strings of 'a', 'b', 'c' with lengths 18, in which no two
consecutive occurrences of b are found, and c's always come in pairs. The
following grammar does it:
ORD
S
--> X X X X X X X X X X X X X X X X X X
----------------------------------------------------------
LIN
X
--> a
#b
X --> #b b
[Negative
context. Never two consecutive 'b']
X
? --> c Y ?
[Can't
be applied if "X" is the rightmost symbol]
Y
X --> c
[This
rule is length-decreasing]
Typical
productions of this grammar are:
b
a a b c c a c c a b a a b a b c c
b
c c b c c c c c c a b a b c c b a
b
c c c c c c c c c c c c c c b a a
a
c c b a c c a a c c c c b c c c c
c
c a a c c a b a c c a a b c c b a
a
b a b a b a c c b a b a a b c c a
b
c c a b a a a c c a b a c c c c b
a
c c c c c c b c c c c a a a c c b
a
a a c c a b c c a c c a b c c c c
The
detailed derivation of the first example is self-explanatory:
S
X
X X X X X X X X X X X X X X X X X
b
X X X X X X X X X X X X X X X X X
b
a X X X X X X X X X X X X X X X X
b
a a X X X X X X X X X X X X X X X
b
a a b X X X X X X X X X X X X X X
b
a a b c Y X X X X X X X X X X X X X
b
a a b c c X X X X X X X X X X X X
b
a a b c c a X X X X X X X X X X X
b
a a b c c a c Y X X X X X X X X X X
b
a a b c c a c c X X X X X X X X X
b
a a b c c a c c a X X X X X X X X
b
a a b c c a c c a b X X X X X X X
b
a a b c c a c c a b a X X X X X X
b
a a b c c a c c a b a a X X X X X
b
a a b c c a c c a b a a b X X X X
b
a a b c c a c c a b a a b a X X X
b
a a b c c a c c a b a a b a b X X
b
a a b c c a c c a b a a b a b c Y X
b
a a b c c a c c a b a a b a b c c
A
"RND" subgrammar instead of a "LIN" subgrammar would yield, for instance
S
X
X X X X X X X X X X X X X X X X X
X
X X b X X X X X X X X X X X X X X
X
X X b X X X X X a X X X X X X X X
X
X X b X X X X X a X X c Y X X X X X
X
X a b X X X X X a X X c Y X X X X X
X
X a b X X X a X a X X c Y X X X X X
X
X a b X X b a X a X X c Y X X X X X
X
X a b X X b a X a X X c c X X X X
X
X a b X b b a X a X X c c X X X X
X
X a b X b b a X a X X c c X X b X
X
X a b X b b a X a b X c c X X b X
X
X a b X b b a X a b X c c X c Y b X
X
X a b X b b a X a b X c c c Y c Y b X
X
X a b X b b a b a b X c c c Y c Y b X
b
X a b X b b a b a b X c c c Y c Y b X
b
X a b X b b a b a b a c c c Y c Y b X
b
a a b X b b a b a b a c c c Y c Y b X
b
a a b a b b a b a b a c c c Y c Y b X
b
a a b a b b a b a b a c c c Y c Y b a
b
a a b a b b a b a b a c c c Y c Y b a
which
(like many context-sensitive grammars) does not produce a terminal derivation.
Each
rule has its own derivation mode.
As suggested above, in "LIN"
grammars the leftmost occurrence of the first argument of the rule is searched
for. However, in "RND"
or "ORD"
grammars the derivation mode needs to be specified. The default derivation
mode, notated "RND", means that the derivation position will be taken randomly
among candidate positions in the work string. If you want to rewrite the
leftmost (resp. rightmost) occurrence of the left argument of the rule, insert
"LEFT"
(resp. "RIGHT")
before the first argument of the rule (after its weight). Note that "LEFT" or
"RIGHT" rules take significantly less computation time.
You
must also keep in mind that a "RND" grammar with "LEFT" rules does necessarily
yield a leftmost derivation. For instance, the following variant of the
"-gr.tryLIN"
grammar
ORD
S
--> X X X X X X X X X X X X X X X X X X
----------------------------------------------------------
RND
LEFT
X --> a
LEFT
#b X --> #b b
LEFT
X ? --> c Y ?
LEFT
Y X --> c
produces
the (incorrect) derivation:
S
X
X X X X X X X X X X X X X X X X X
b
X X X X X X X X X X X X X X X X X
b
a X X X X X X X X X X X X X X X X
b
a a X X X X X X X X X X X X X X X
b
a a b X X X X X X X X X X X X X X
b
a a b c Y X X X X X X X X X X X X X
b
a a b c Y a X X X X X X X X X X X X
[Here
it failed because "X --> a" was also candidate]
b
a a b c Y a c Y X X X X X X X X X X X
b
a a b c Y a c Y a X X X X X X X X X X
b
a a b c Y a c Y a b X X X X X X X X X
b
a a b c Y a c Y a b a X X X X X X X X
b
a a b c Y a c Y a b a a X X X X X X X
b
a a b c Y a c Y a b a a b X X X X X X
b
a a b c Y a c Y a b a a b a X X X X X
b
a a b c Y a c Y a b a a b a b X X X X
b
a a b c Y a c Y a b a a b a b c Y X X X
b
a a b c Y a c Y a b a a b a b c Y c Y X X
b
a a b c Y a c Y a b a a b a b c Y c c X
b
a a b c Y a c Y a b a a b a b c Y c c b
b
a a b c Y a c Y a b a a b a b c Y c c b
A
partial control of derivations is possible either after an interruption or
before starting a production, by choosing the "Step-by-step" and "Select
candidates" options. (See QuickStart §12)
4.5 Destroying
structures
Consider
the three-level
pattern
grammar
(see "-gr.tryDESTRU"):
RND
<2-1>
S --> (= (= X) S (:X)) (: (= X) S (:X))
<2-1>
X --> Y
<2-1>
X --> Y S Z
<2-1>
X --> Z
----------------------------------------
ORD
LEFT
S
--> lambda
----------------------------------------
LIN
[A
line is missing here...]
X
X --> abca
Z
Y --> abc
Y
Z --> cba
Y
Y --> cbbc
Z
Z --> lambda
This
grammar would not produce strings of terminal symbols because the first
subgrammar produces strings of X's and Y's mixed with structural symbols "(=",
"(:", ")". These symbols should be deleted before subgrammar #3 is applied.
Procedure "_destru"
takes care of it. This instruction should be placed on top of the third
subgrammar:
LIN
_destru
X
X --> abca
Z
Y --> abc
...
With
the "_destru" procedure, terminal strings on the alphabet {a,b,c} are
generated, for instance:
cbbcabcabcabcabccbbcabcabcabcabc
abcabcabcabcabcabcabcabc
cbacbbccbbccbacbacbbccbbccba
cbacbacbacba
cbaabccbaabc
cbbccbbccbbccbbccbbccbbc
abcabcabcabcabcabcabcabc
4.6 Weights
A
weight
in range [0, 32767] may be attached to each rule. They are used when several
rules are candidates in "RND", "LIN", "SUB" or "SUB1" grammars. A rule with
weight <0> is
inactive.
The weight value is indicated between angle brackets, e.g. <43>.
Default weight is <127>. It is convenient to use weights in range 0..127
so that they may be set by MIDI controllers, using parameters K1, K2... (see
QuickStart §6).
Weights
may be
dynamically
controlled:
any rule may gain a positive or negative weight increment each time it is
applied. For instance, a rule with weight <100-30> will have successive
weights 100, 70, 40, 10 and 0, and therefore cannot be applied more than four
times in the same production.
A
good idea for checking a grammar is to set the weights of some rules to
<1-1> (or <n-n> for any integer
n).
These rules can be used only one time. Once an item has been produced,
produce a new one without resetting rule weights (the option is available by
typing cmd-option space): the next item will be based on different rules since
former ones have become inactive.
When
using a subgrammar with dynamically decrementing weights, derivations of the
work string stop when all candidate rules have weight <0>. This is a
common way of avoiding endless derivations.
Changing
weights dynamically on context-sensitive rules is a simple way to let patterns
"emerge" randomly: some rules are becoming more active while they "inhibit"
others.
Weights
may be
infinite.
This
is necessary when a rule should absolutely be applied as soon as it becomes a
candidate. (BP2 actually selects the
first
candidate rule with an infinite weight)
An infinite weight is notated "<∞>". On US keyboards, character
'∞' is obtained by typing '5' with the 'option' key down.
4.7 Metavariables
Wild
cards notated '?1', '?2', etc. may be used in production rules. A wild card
may be replaced with any terminal symbol, simple note, variable, bracket,
out-time object, synchronisation tag, time-pattern or performance parameter.
For example, a rule like
?1
?2 ?3 ?1 --> (= ?1) (= ?2) ?3 * (: ?2) (: ?1)
rewrites
"X Y Z X" as "(= X) (= Y) Z * (: Y) (: X)". (Symbol '*' is an homomorphism.)
'?'
is an old notation that may be replaced with '?n' for any value of n.
4.8 Tempo
and gaps
If
no indication is given, a sequence of symbols is interpreted as "one symbol per
time unit". We mean
symbolic
time units counted on a
symbolic
tempo.
Sound-object sequence "a b c d e f" may also be notated "/1 a b c d", where
"/1" is called an
explicit
tempo marker.
Similarly, if the same sequence is to be interpreted three times faster it is
notated "/3 a b c d e f".
Using
explicit tempo markers makes it possible to change tempo within the string.
For instance, in sequence
/2
a b c d e f /3 g h i j k l m n o
'a'
... 'f' are interpreted at speed 2 (two sound-objects per beat) while 'g' to
'o' are interpreted at speed 3. (This may also be viewed as a tempo
acceleration of 3/2.) If '_' (empty sound-object) is used to denote a
prolongation of the preceding object, the same expression may equivalently be
notated:
/6
a_ _ b_ _ c_ _ d_ _ e_ _ f_ _ g_ h_ i_ j_ k_ l_ m_ n_ o_
Gaps
(silences
or rests) are written as hyphens or integer numbers. The following notations
are equivalent:
/2
a b - - c d /3 e - - - - f g h
/2
a b 2 c d /3 e 4 f g h
Rational
numbers may also be used to indicate
fractional
gaps,
e.g.
/1
a b /2 c d e f 4/3 g h
in
which 'a' and 'b' are interpreted at speed one, 'c', 'd', 'e', 'f', "g" and
"h" at speed two while sequences "cdef" and "gh" are separated with a silence
of duration 4/3. Since the "4/3" silence occurs at speed two its actual
symbolic duration
is 4/3 x 1/2 = 2/3. Here again BP2 will expand the representation to
/6
a _ _ _ _ _ b _ _ _ _ _ c _ _ d _ _ e _ _ f _ _ - - - - g _ _ h _ _
where
the "4/3" gap is represented as "- - - -" (or "- _ _ _" equivalently). The
following representations are equivalent:
/6
a _ _ _ _ _ b _ _ _ _ _ c _ _ d _ _ e _ _ f _ _ - _ _ _ g _ _ h _ _
/6
a _ _ _ _ _ b _ _ _ _ _ c _ _ d _ _ e _ _ f _ _ 4 g _ _ h _ _
4.9 Object
concatenation
Normally
a string "abcb" represents a sequence of objects 'a','b','c' such that:
'b'
starts at the moment 'a' stops; 'c' starts at the moment 'b' stops; 'b' starts
again at the moment 'c' stops.
What
if we want 'b' to continue while 'c' is on? In other words, we wish to
represent:
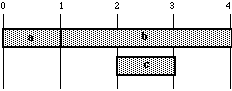 Fig.5
Using the concatenation symbol
Fig.5
Using the concatenation symbol
This
can be done using the
concatenation
symbol
'&'. The proper representation is
a
b& c &b
Beware
that spaces are meaningful in this representation: you can't write "b&c".
More complex structures can be defined in a similar way. For instance,
a
b& c& d c &c b &b
may
be interpreted as:
 Fig.6
Using the concatenation symbol (more complex)
Fig.6
Using the concatenation symbol (more complex)
Object
concatenation
is used for representing objects which belong to several substructures, i.e.
that are not structured as a tree hierarchy. See for instance the grammar
generating Ames' example in §4.10.
4.10 Polymetric
expressions
Polymetric
expressions
are useful for string representations of
polyphonic
music.
A simple polymetric expression
is shown figure 7 in staff notation, BP2 graphics and
phase
diagram
.
The latter is a table containing pointers to the instances of sound-objects
'C4', 'E#3', etc.
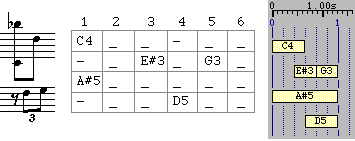 Fig.7
Staff notation, phase diagram
and BP2 graphic display of a polymetric expression
notated "{1, C4 -, - E#3 G3, A#5, - D5}"
Fig.7
Staff notation, phase diagram
and BP2 graphic display of a polymetric expression
notated "{1, C4 -, - E#3 G3, A#5, - D5}"
This
expression is notated "{1, C4 -, - E#3 G3, A#5, - D5}" on a BP2 text score.
It shows five sequences (
fields)
separated by commas. The leftmost field contains '1', the
symbolic
duration
of the expression. With a metronome set to 45 beats per minute, the resulting
physical duration is 1.33 seconds.
The
polymetric
expansion algorithm
imbedded in Bol Processor coerces all sequences of the structure to the same
symbolic duration. The second field contains a note 'C4' followed by a silence
'-', both of which will be treated as quavers. The third field contains the
sequence "- E#3 G3" which is performed as a triplet.
Thus,
the polymetric expression
"{1, C4 -, - E#3 G3, A#5, - D5}" is expanded to "/6 {C4_ _ -_ _,-_ E#3_
G3_,A#5_ _ _ _ _,-_ _ D5_ _}" as suggested by the phase diagram. Symbol '_' is
a prolongation of the preceding sound-object, and '/6' indicates a change of
tempo after which durations are divided by 6.
The
phrase shown figure 7 is an excerpt of a musical example imitating Steve
Reich's style. A grammar generating examples in this style, composed by
Thierry Montaudon, is shown fig.8.
S
--> _velcont _vel(50) Part1 Part2 Part3
Part1
--> A A A A A A A A
Part2
--> B B B' B' C C D D D D E E E E
Part3
--> C C C D E E E E C D C D E E E E C C C B' B' B A A A A A
A
--> {1, C4 -,_vel(40) - E#3 G3, A#5, - D5}
B
--> {A A, _vel(60) C2}
B'
--> {B, - F5}
C
--> {B, _vel(55) - C5}
D
--> {B, - C4 F5 E#4}
E
--> {D, D#4 F4 C5 G#3}
Fig.8
A grammar producing a piece
à
la
Steve Reich
In
this grammar, velocities are set by controls "_vel(x)" and are interpolated
throughout the piece due to instruction "_velcont". The upper four rules
define the deep structure of the piece. The lower ones use variables 'A', 'B',
'C'... to construct polymetric structures stringed together in each part of the
piece.
Consider
another example. Let {a b , c d e} be a sound structure in which two
sound-object sequences: "a b" and "c d e" are superimposed. The interpretation
chosen by BP2 is
{a
_ _ b _ _ , c _ d _ e _}
in
which '_' is a prolongation of the preceding sound-object. The two sequences
may be written on a two-line phase diagram
which
exclusively states that
'a' starts with 'c', 'd' starts before 'b' which in turn starts before 'e'...
The
interpretation of this polymetric expression
automatically sets the tempo of "cde" at a speed which is 3/2 that of "ab".
This property may be used for indicating any fractional relative change of
tempo. For example,
/1
{4, a b c - - } {2, d e f} {5/3, g h}
indicates
that sequence "a b c - -" must be adjusted to fit exactly within 4 beats, then
"d e f" within 2 beats, then "g h" within 5/3 beats. BP2 performs the
necessary calculations and stretches the final representation. The fact that a
representation is ‘stretched’ does not mean it will be played
slower. BP2 calculates a time-scale factor to adjust its duration accordingly.
Integers,
fractions or hyphens indicating durations must appear in the
first
field of a polymetric expression,
because if an expression contains no explicit tempo marker its default duration
is that of the first field. Compare for instance
/1
a b {c d, e f g} h i = /3 a _ _ b _ _ {c _ _ d _ _ , e _ f _ g _ } h _
_ i _ _
with:
/1
a b {e f g , c d} h i = /2 a _ b _ {e _ f _ g _ , c _ _ d _ _ } h _ i _
Another
feature useful for dealing with polymetric structures is the handling of
undetermined
rests:
notated '_rest' or '...' (Use option semi-colon on a US keyboard, never type
three periods) Each field in a polymetric expression
may contain one undetermined rest appearing anywhere in the sequence. BP2
first determines the structure ignoring fields with undetermined rests, then it
scans again fields with undetermined rests. Some among them have fixed
durations because they contain an explicit tempo marker, e.g.:
{/1
fa5 {la5 si5,do6 re6 mi6}, do1 _rest /2 fa1 }
in
which the second field contains "/2", i.e. two sound-objects per time unit. It
also means that "do1" should be performed at (default)
one-sound-object-per-time-unit tempo, which is formally notated:
{/1
fa5 {la5 si5,do6 re6 mi6}, /1 do1 _rest /2 fa1 }
The
symbolic duration of the first field (hence, of the second field as well) is
that of sequence "/1 fa5 la5 si5", i.e. three units. The duration of the
second field is 3/2 units plus the undetermined rest. Therefore the
undetermined rest is also 3/2 units, which could have been written:
{/1
fa5 {la5 si5,do6 re6 mi6}, do1 3/2 /2 fa1 }
An
error message is generated if there is insufficient time for a rest. An
undetermined rest is meant to yield the
simplest
possible expression. For example,
{fa5 {la5 si5,do6 re6 mi6}, do1 re1 mi1 ... fa1 }
=
{fa5 {la5 si5,do6 re6 mi6}, do1 re1 mi1 - - fa1 }
=
{fa5 _ {la5 _ si5 _ , do6 _ re6 _ mi6 _ }, do1 re1 mi1 - - fa1 }
(See
Bel 1990a, 1991, 1992).
Let
us now compare polymetric expressions
with
event
tables
used in MIDI sequencers. The following musical fragment is borrowed from the
COMPOSE
Tutorial and Cookbook
(Ames
1989:2):
 Fig.9
Score display
Fig.9
Score display
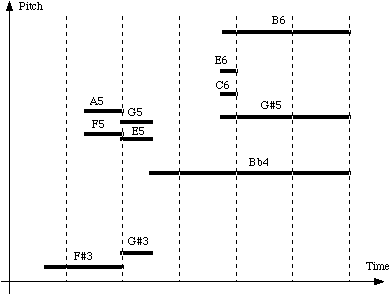 Fig.10
Piano-roll display
Fig.10
Piano-roll display
The
list of events for this example is given in the
event
table
(ibid:3):
|
Period
.667
.667
.667
.5
1.25
0
2.25
|
Duration
.667
1.333
.667
.5
3.5
2.25
.25
|
Pitch
R
[rest]
F#3
F5:A5
G#3:E5:G5
Bb4
C6:E6
G#5:B6
|
where
"period" stands for the time elapsed from the on-setting of a note (or rest or
chord) to the on-setting of its successor.
A
possible (yet arguable) structural analysis of this example is
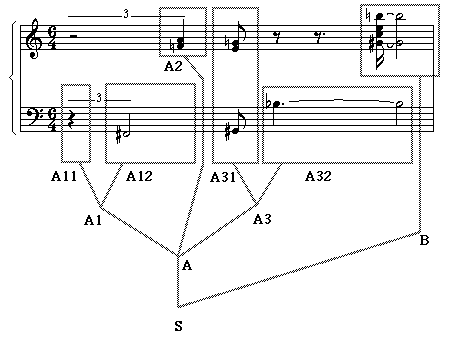 Fig.11
A structural analysis
Fig.11
A structural analysis
The
score shown Fig.11 may be generated by the following grammar. Variables A1,
A2, etc. must be written between vertical bars so that they are not confused
with terminal symbols (musical notes A1, A2, etc.).
S
--> {|A|,... |B|}
A
--> {2, |A1|,2 |A2|} {4, |A3|}
|A1|
--> {|A11| ..., - |A12|}
|A3|
--> |A31| |A32|
|A11|
--> -
|A12|
--> {2,F#3}
|A2|
--> {F5,A5}
|A31|
--> {1/2,G#3,E5,G5}
|A32|
--> {3/2,Bb4&} {2,&Bb4}
B
--> {1/4,G#5&,C6,E6,B6&} {2,&G#5,&B6}
...
(other rules in the same grammar)
yielding
a unique derivation:
{{2
,{- ...,-{2 ,F#3}},2 {F5,A5}}{4 ,{1 /2 ,G#3,E5,G5}{3 /2 ,Bb4&}{2
,&Bb4}},...{1 /4 ,G#5&,C6,E6,B6&}{2 ,&G#5,&B6}}
Time
information is redundant in this representation (evidently, 4 = 1/2 + 3/2 + 2),
but it is consistent. BP2 will produce the following expanded representation
/12{{-_
_ _ _ _ _ _ F#3_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,-_ _ _ _ _ _ _ -_ _ _ _ _ _ _
{F5_ _ _ _ _ _ _ ,A5_ _ _ _ _ _ _ }}{G#3_ _ _ _ _ ,E5_ _ _ _ _ ,G5_ _ _ _ _
}Bb4_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ & &Bb4_ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ ,-_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _ -_ _
-_ _ -_ _ -_ _ -_ _ -_ _ {G#5_ _ &,C6_ _ ,E6_ _ ,B6_ _ &}{&G#5_
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,&B6_ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ }}
which
is internally represented:
/12
{/12 {/6 /18 - /9 F#3 /18 /6 ,/18 - -{/18 F5,/18 A5}/18 }/12 /12 {/24 G#3,/24
E5,/24 G5}/12 /8 Bb4&/12 /6 &Bb4 /12 /12 ,/12 /48 - - - - - - - - - - -
- - - - /12 {/48 G#5&,/48 C6,/48 E6,/48 B6&}/12 {/6 &G#5,/6
&B6}/12 }/12
The
philosophy behind polymetric representation
is that it should contain a minimum amount of time information, for two major
reasons:
- there
is a lot of time information that the machine is able to calculate, for
instance here the duration of chord {F5, A5};
- timing
information should be based on final items, therefore on contextual information
regarding tempo.
4.11 Period
notation
In
the same way it deals with superimposed sequences, the polymetric expansion
algorithm works out equal symbolic durations between beat separators notated
'•' -- the "period notation." A note sequence in period notation and the
context-free grammar it originated from (composed by Harm Visser) are shown
Fig.12. See "-gr.acceleration"
in the VISSER & MONTAUDON folder.
In
this example, beats contain increasing numbers of notes resulting in an
accelerating movement. Velocity assignments have of course no effect on
durations.
S
-->
_vel(60)
A B _vel(65) C D _vel(70) E F _vel(75) G _vel(77) H _vel(80) I _vel(85) J
_vel(87) K _vel(90) L
A
--> E2 •
B
--> D2 A
C
--> B2 B
D
--> G2 C
E
--> F#2 D
F
--> A#2 E
G
--> C2 F
H
--> G#2 G
I
--> A2 H
J
--> D#2 I
K
--> C#2 J
L
--> F2 K
BP2
score:
Velocity
controls have been left out
E2
• D2 E2 • B2 D2 E2 • G2 B2 D2 E2 • F#2 G2 B2 D2 E2
• A#2 F#2 G2 B2 D2 E2 • C2 A#2 F#2 G2 B2 D2 E2 • G#2 C2 A#2
F#2 G2 B2 D2 E2 • A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 • D#2 A2 G#2 C2 A#2
F#2 G2 B2 D2 E2 • C#2 D#2 A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 • F2 C#2
D#2 A2 G#2 C2 A#2 F#2 G2 B2 D2 E2 •
Fig.
12 A grammar producing an accelerating sequence of notes, and the resulting
item in BP2 score notation
Once
the grammar has been typed, the user may select "Produce items" to get a text
or graphic display of its production, listen to it on the MIDI output, and
optionally produce a Csound score. The output of the "acceleration grammar" of
figure 2 is displayed on a piano-roll score:
 Fig.13
A piano-roll of the item produced by the grammar of Fig.12
Fig.13
A piano-roll of the item produced by the grammar of Fig.12
4.12 Remote
context
Standard
formal (Chomsky) grammars make it very difficult (although theoretically
possible) to control productions on the basis of a
remote
context,
i.e. the occurrence of a string located
anywhere
to the left or right side of the derivation position. Therefore a special
syntax of remote contexts is available in BP2.
Remote
contexts are represented between ordinary brackets in the left argument of a rule.
These brackets are not confused with pattern delimiters because they neither
contain '=' nor ':'.
For
instance, a rule like
(a
b c) X Y (c d) --> X e f
means
that "X Y" may be rewritten as "X e f" only if "a b c" is found somewhere
before "X Y" in the string under derivation, and "c d" somewhere after "X Y".
Note that "X" itself is a left context in the sense of conventional generative
grammars.
A
remote context
may contain any string in BP syntax, including string patterns and
metavariables. It may also be negative. For instance,
#(a
b c) X --> c d e
means
that "X" may be rewritten as "c d e" only if not preceded by "a b c" in the
string under derivation.
Below
is a typical grammar using remote contexts (see "-gr.bells").
The problem was to generate sequences of permutations of 'a', 'b', 'c', 'd',
using simple transformations, given that sequences are never repeated. (This
problem is borrowed from the traditional art of composing bell-ringing tunes,
see Bel 1990c,1992) The sequence must begin and end with "ABCD", hence the
infinite-weight rule that terminates the generation.
RND
S
--> /4 Tune
Tune
--> Canonic New B A C D X12
End
Tune
--> Canonic New A C B D X23
End
Tune
--> Canonic New A B D C X34
End
Tune
--> Canonic New B A D C X1234
End
----------------------------------------------------------
LIN
<∞>
A B C D ?1 End --> A B C D [Infinite weight]
#(?1 ?2 ?4 ?3) ?1 ?2 ?3 ?4 X12 --> ?1 ?2 ?3 ?4 New ?1 ?2 ?4 ?3
X34
#(?2 ?1 ?4 ?3) ?1 ?2 ?3 ?4 X12 --> ?1 ?2 ?3 ?4 New ?2 ?1 ?4 ?3
X1234
#(?2 ?1 ?4 ?3) ?1 ?2 ?3 ?4 X34 --> ?1 ?2 ?3 ?4 New ?2 ?1 ?4 ?3
X1234
#(?2 ?1 ?3 ?4) ?1 ?2 ?3 ?4 X34 --> ?1 ?2 ?3 ?4 New ?2 ?1 ?3 ?4
X12
#(?2 ?1 ?4 ?3) ?1 ?2 ?3 ?4 X23 --> ?1 ?2 ?3 ?4 New ?2 ?1 ?4 ?3
X1234
#(?2 ?1 ?3 ?4) ?1 ?2 ?3 ?4 X1234 --> ?1 ?2 ?3 ?4 New ?2 ?1 ?3 ?4
X12
#(?1 ?3 ?2 ?4) ?1 ?2 ?3 ?4 X1234 --> ?1 ?2 ?3 ?4 New ?1 ?3 ?2 ?4
X23
#(?1 ?2 ?4 ?3) ?1 ?2 ?3 ?4 X1234 --> ?1 ?2 ?3 ?4 New ?1 ?2 ?4 ?3
X34
-----------------------------------------------------------
ORD
[These
rules are needed in case the infinite-weight rule could not be applied]
LEFT
X12 --> lambda
LEFT
X34 --> lambda
LEFT
X23 --> lambda
LEFT
X1234 --> lambda
LEFT
End --> lambda
LEFT
New --> lambda
LEFT
Canonic --> A B C D
-----------------------------------------------------------
SUB
[Tuning
bells... See substitutions §4.14]
A
B --> do3 B
A
#B --> do4 #B
B
--> sol3
B
--> sol4
C
--> re4
C
--> re5
D
A --> mi4 A
D
#A --> mi5 #A
4.13 Metagrammars
All
symbols used for representing a grammar may be the terminals of a
metagrammar
whose role is to generate a set of (related) grammars. For instance, the
following metagrammar
RND
[A grammar is a set of rules]
<1>
S --> 'RND'; Ri
<10>
S --> S ; R
----------------------
RND
[Define context-free rules in Chomsky normal form]
Ri
--> 'S' '-->' Arg2
R
--> Arg1 '-->' Arg2
Arg1
--> Variable
<1>
Arg2 --> Constant
<5>
Arg2 --> Variable Variable
------------------------
RND
Variable
--> X
Variable
--> Y
Variable
--> Z
Constant
--> a
Constant
--> b
Constant
--> c
Constant
--> d
generates
any
l-free
context-free grammar with variables {X,Y,Z} and terminal symbols {a,b,c,d}.
'S', 'RND' and '-->' are terminal symbols of the metagrammar itself, hence
the single quotes. Semicolons generated by this grammar are automatically
converted to line feeds.
Most
grammars generated by "-gr.gramgene1"
produce empty languages. There are better ways of producing grammars. A
grammar called "-gr.gramgene2"
on the BP2 disk may be used to generate (non-empty-language) pattern grammars
such as for instance:
-ho.abc
RND
S --> Y Z
Y --> X X
Z --> X X
Y --> b
Z --> d
Y --> c
Z --> (=(= Z )(: Z ))(:(= Z )(: Z )) Y
Y --> d
Z --> X X
X --> b
X --> X Z
X --> a
X --> (= X )(: X ) Y
4.14 Substitutions
"SUB"
grammars perform simultaneous rewriting of symbols in the work string. For
instance,
SUB
S
-->
A
B B A B B A
A
B
-->
a B
B
A
-->
B
b
A
A
-->
c
c
A
B A
-->
A
d A
B
B A
-->
B
e A
B
B
-->
f
B
produces
string "afeafeb" in one single "
parallel
derivation". The
string "ABBABBA" is rewritten "afeafeb" as shown Fig.14.
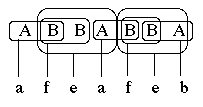 Fig.14
A substitution in a "SUB" grammar
Fig.14
A substitution in a "SUB" grammar
Substitutions
may be used for designing a general category of unidimensional cellular automata
and some multidimensional ones.
If
substitutions are performed on strings of terminal symbols, each step may
produce an interesting sound-object sequence. For this reason, it is possible
to instruct BP2 to play all substitutions
in the "Improvize" mode. The option is given in the "Settings" dialog. See an
application in "-gr.koto3".