Adresse de ce document: <http://www.lpl.univ-aix.fr/~belbernard/music/projects/mbrola.htm>
Révision 25 mars 1999

Activités en cours / current work
Références
Annexes

Représentation de structures temporelles dans un environnement de synthèse de la parole

Bernard Bel

Il existe une affinité entre les projets de réalisation d'un synthétiseur de parole multilingue et d'un synthétiseur de son musicaux basés sur des algorithmes programmés dans lesquels la connaissance spécifique (de la langue ou du système musical) se distingue clairement de la connaissance générique (de traitement du signal). Le projet MBROLA <http://tcts.fpms.ac.be/synthesis/> peut à ce titre être comparé au projet Csound <http://www.leeds.ac.uk/music/Man/c_front.html>:

• MBROLA est un environnement multilingue; de même, Csound ne fait pas d'impasse sur les styles et genres musicaux;
• La connaissance spécifique permettant, au niveau acoustique, de produire le signal de parole, est introduite dans MBROLA à partir de bases de données de diphones établies pour une langue et un locuteur spécifiques. Ces bases de données sont similaires aux orchestra files de Csound, avec une différence notable que les dernières ne sont que des descriptions algorithmiques de procédures de synthèse ou de transformations de signaux (les instruments);
• La description symbolique-numérique du signal à synthétiser se fait, dans les deux environnements, à l'aide de fichiers texte contenant des listes d'événements marqués temporellement et complétés par des paramètres de "contrôle", par exemple les paramètres de fréquence et d'intensité générés par les règles phonotactiques en synthèse de parole;
• Les deux environnements sont développés de manière coopérative, avec une précaution dans le cas de MBROLA qui centralise la compilation des bases de données. (Csound est distribué par le MIT Media lab avec le code source libre de droits. Les enjeux scientifiques et commerciaux de la synthèse musicale et de la synthèse de la parole sont de toute autre nature.)

Structures temporelles pour la synthèse musicale

Un problème commun à la synthèse de parole et la synthèse musicale est celui de la description de structures temporelles permettant de déterminer, de manière déterministe ou partiellement stochastique, les dates des "objets sonores" (ou des unités phonétiques). Mon travail sur les structures musicales (cf. Bel 1990b, Bel 1992a) a consisté en premier lieu à distinguer deux niveaux de représentation:

• Le niveau symbolique du musical score, où la structure musicale est entièrement décrite par une expression polymétrique (définie récursivement comme une séquence d'objets sonores ou une superposition d'expressions polymétriques). Il s'agit d'une structure d'unités discrètes: objets sonores et opérateurs de modification de paramètres (performance controls). Un objet sonore des plus simples, en musique, est une note. Un performance control peut modifier un paramètre arbitraire de génération/transformation du signal.
• Le niveau physique, sur lequel les objets sonores sont "instanciés", c'est à dire remplacés par des séquences de messages (événements) envoyés au synthétiseur, complétés par des messages de modification des paramètres.

Il convient, de la même manière, de distinguer entre temps symbolique et temps physique.

• Le temps symbolique est celui de la partition musicale (score). Il est intéressant de le noter avec des fractions entières pour déterminer sans ambiguité les coincidences temporelles dans une structure polyphonique. Par contre, il ne décrit pas nécessairement toutes les relations de précédence. La grammaire musicale peut décider qu'une structure polymétrique superposera plusieurs séquences de nombres inégaux d'objets sonores, sans pour autant déterminer a priori toutes leurs relations de précédence temporelle. (Voir Structures polymétriques en annexe). De même, une séquence peut contenir un certain nombre de temps (beats) dont les durées devront être automatiquement ajustées à des valeurs égales. (Voir Period notation en annexe)
• Le temps physique est le temps réel de la performance. Il peut être représenté sur une échelle réelle (nombres en virgule flottante). Il permet d'ordonner strictement tous les événements et de fixer leurs durées pour un contexte de performance donné.

La correspondance (mapping) entre le temps symbolique et le temps réel peut être aussi complexe qu'on le souhaite, bien que l'on adopte de préférence une fonction monotone. En musique on établir une distinction entre le temps strié, celui qui est défini par une "battue" (métronomique ou non) et le temps lisse, pour lequel les "stries" temporelles sont déterminées par la durée de certains objets sonores. (Les termes "temps strié" et "temps lisse" ont été empruntés à Boulez.)

Niveau symbolique: l'expansion polymétrique

David Jaffe et plusieurs concepteurs de logiciels de composition musicale utilisent des fonctions numériques de warping entre le temps symbolique ("virtuel" dans le vocabulaire de Jaffe) et le temps physique. Une fonction numérique permet de représenter directement des variations arbitraires de tempo. Le problème est que, n'étant pas intégrée à la définition "syntaxique" de la pièce musicale, elle reste un dispositif de contrôle extérieur. Je propose une représentation différente au niveau syntaxique (celui du score d'unités discrètes sur le temps symbolique):

1. Les variations de vitesse sont exprimées par l'opérateur _tempo(x), où 'x' est un nombre fractionnaire ou en virgule flottante. Dans ce dernier cas, l'algorithme d'expansion polymétrique le convertit en fraction entière pour respecter le format des durées symboliques rationnelles. Par exemple,

   A3 B3 _tempo(1.5) C4 D4 _tempo(1/2) E4 F4

   dans lequel les notes/objets sonores A3 et B3 sont exécutées à la vitesse 1, C4 et D4 à la vitesse 3/2, et E4, F4 à la vitesse 1/2. Cet opérateur se combine bien entendu avec la period notation et la notation polymétrique de séquences superposées.
2. Les time-patterns, objets "temporels" simplifiés, permettent de définir des rapports de durées arbitraires pour structurer les stries temporelles dans une pièce musicale interprétée en temps lisse. (Voir Time-patterns en annexe.)
3. Il est utile de pouvoir insérer dans toute séquence des silences de durée indéterminée (notés _rest) que l'algorithme se charge d'évaluer en respectant une consigne de complexité minimale.

L'algorithme d'expansion polymétrique est amené à effectuer des opérations complexes sur des fractions entières (notamment des calculs de PPCM et PGCD) au cours desquelles les entiers peuvent dépasser les valeurs limites de la représentation en machine. C'est pourquoi les fractions peuvent subir des approximations dès qu'un de leurs termes dépasse une valeur déterminée.

Pour réaliser l'instanciation des objets (étape suivante, voir infra) il est nécessaire de construire un diagramme de phases, tableau bidimensionnel qui contient autant de lignes que de séquences superposées, et autant de colonnes que de stries temporelles. Pour une durée totale donnée, le nombre de stries temporelles peut varier considérablement en fonction de la "granularité" imposée par l'expansion polymétrique -- car les PPCM peuvent croître indéfiniment et atteindre des valeurs considérables, même pour des structures musicales simples en apparence. Or une granularité fine n'est pas toujours indispensable. Si l'on fournit une valeur minimum significative de quantification (quantization), typiquement 10 à 30 millisecondes, le diagramme de phases peut être simplifié en fusionnant les colonnes séparées d'une distance temporelle inférieure à la quantification. Cette simplification s'effectue au niveau symbolique, c'est à dire avant la construction du diagramme de phases (et la mobilisation d'une quantité de mémoire proportionnelle au nombre de colonnes). (Voir Bel 1998)

La quantification permet d'économiser de l'espace mémoire (et accessoirement du temps de calcul) dans un rapport qui dépasse fréquemment une dizaine de milliards pour des pièces musicales relativement simples. C'est le cas par exemple de la pièce "Waves" d'Harm Visser (1998) (écouter l'example sonore).

Niveau physique: l'instanciation des objets sonores

Le passage de la description symbolique -- le musical score, séquence de symboles discrets -- à la description physique, une séquence d'événements MIDI ou Csound, se fait par un algorithme de résolution de contraintes: l'instanciation des objets sonores. Les objets sonores ne sont pas seulement des listes marquées temporellement d'événements élémentaires. Tout objet sonore peut être enrichi de propriétés qui servent à construire un système de contraintes que devra résoudre l'algorithme d'instanciation.

Je distingue:

• Les propriétés métriques, qui définissent dans quelles limites l'objet peut être contracté ou dilaté lorsque la vitesse de la performance varie;
• Les propriétés topologiques, qui définissent les relations que l'objet peut entretenir avec les objets voisins sur l'axe temporel. En bref:
  • Quelle fraction du début et de la fin de l'objet pourrait être recouverte par un objet voisin? Cette fraction aussi peut être négative si l'objet doit toujours être précédé ou suivi d'un silence;
  • Existe-t-il une valeur de silence maximum précédant ou suivant un objet? Un silence nul est par exemple une contrainte de continuité;
  • Quelle fraction du début et de la fin de l'objet pourrait-elle être tronquée pour résoudre une contrainte de non-recouvrement?
  • Chaque objet possède un pivot temporel qui permet de le situer par rapport à la strie temporelle qui lui sera affectée lors de son instanciation. Le pivot est par défaut au début de l'objet, mais il peut être déplacé arbitrairement, notamment lorsqu'il dénote un instant de climax plus significatif que le début de l'objet.
  • L'objet peut-il être déplacé sur l'axe temporel, et dans quelles limites?
  • Les valeurs du pre-roll et du post-roll de l'objet -- termes empruntés au montage vidéo -- permettent de distinguer l'intervalle temporel attribué à l'objet de celui qui relie la date du premier événement à celle du dernier. Sur le plan pratique, un pre-roll positif permet par exemple d'envoyer la séquence de messages avec suffisamment d'avance pour compenser des retards dans un instrument de musique électromécanique.
  • Certains objets peuvent être cycliques. Au lieu d'être élongués ils sont répétés en boucle à partir d'un point précis qui n'est pas nécessairement leur début.

Pour les propriétés topologiques, les informations temporelles peuvent être exprimées de manière absolue (en millisecondes) ou relative (en pourcentage de la durée physique de l'objet après son instanciation).

Les prototypes d'objets sonores contiennent bien entendu les séquences d'événements élémentaires qui permettront leur réalisation sonore. Ces séquences peuvent être des listes de messages MIDI, des scores Csound, ou une combinaison des deux: on peut définir des objets duaux MIDI/Csound, par exemple en convertissant automatiquement la séquence MIDI en score Csound à l'aide de définitions formelles des instruments Csound affectés à chaque canal MIDI.

(Voir Bel 1992a pour plus de précisions)

Dans l'avenir, les objets sonores pourront aussi contenir des fichiers sonores dans les formats AIFF, QuickTime ou MOD.

Des performance controls temporels notés _legato(x) et _staccato(x) permettent d'allonger ou de raccourcir les objets sonores, et peuvent faire l'objet d'interpolations comme indiqué en annexe (voir Stepwise control of articulation).

Globalement, la production d'une pièce musicale fait donc intervenir un processus top-down pour la génération du score, et un processus bottom-up pour l'instanciation des objets sonores à partir des propriétés de leurs prototypes. Il peut exister un grand nombre de solutions du système de contraintes gérées lors de l'instanciation des objets sonores. Dans ce cas, il est possible d'énumérer les solutions et de choisir la plus proche du résultat désiré.

La performance

Etant donné un musical score et une collection de prototypes d'objets sonores munis de leurs propriétés métriques et topologiques, l'algorithme d'instanciation propose une mise en temps précise des objets désignés dans le score. De plus, il prépare des streams de variations de paramètres continus: le pitchbend (fréquence), la pression, la modulation, le volume et le panoramique (gauche/droite) conventionnels de MIDI, plus un nombre illimité de paramètres arbitraires que l'on peut gérer dans l'environnement Csound. (Voir Bel 1996)

La sortie peut être, selon les options:

• Un flot de messages MIDI envoyés en temps réel à un studio MIDI ou interprétés par le QuickTime Music de MacOS;
• Un fichier MIDI qui peut être ensuite repris avec un autre logiciel;
• Un fichier texte Csound score qui peut être ultérieurement transformé en fichier sonore par Csound;
• Un nouveau prototype d'objet sonore.

Les options précédentes sont souvent combinées: une sortie MIDI en temps réel est souvent suivie de l'enregistrement d'un fichier MIDI. De même, une pièce musicale en Csound peut être pré-écoutée en temps réel avec un dispositif MIDI si tous ses objets sont définis de manière duale MIDI/Csound.

Le contrôle des paramètres continus

Ce contrôle s'effectue de manière différente sous MIDI et sous Csound.

MIDI est un environnement temps réel. Il est donc nécessaire, pendant la performance, d'insérer en temps réel les messages modifiant les valeurs de pitchbend, modulation, volume, ..., chaque fois que ces valeurs doivent être modifiées sur un canal MIDI. Pour éviter la saturation, une fréquence maximale de mise à jour (de l'ordre de 10 à 30 messages par seconde) peut être spécifiée.

Les scores Csound contiennent des listes d'événements discrets (par exemple, des notes). Chaque événement est localisé temporellement par ses dates de début et de fin. Si un paramètre doit varier pendant cet intervalle temporel, il faut fournit les valeurs de début et de fin (cas d'une variation linéaire) ou un pointeur vers un tableau de variations (cas d'une variation plus complexe).

Les variations de paramètres sont représentées, au niveau symbolique, par des opérateurs (_pitchbend(x), _mod(x)...) entre lesquels les valeurs peuvent être déterminées par interpolation si l'on insère une instruction (_pitchcont, _modcont...) en début de séquence. On peut aussi réaliser des variations graduelles grâce aux instructions: _pitchstep, _modstep... Dans ce dernier cas, le paramètre reste constant sur l'étendue de chaque objet sonore (voir Bel 1996). A chaque paramètre "actif" est affectée une structure de données (stream) contenant les informations nécessaires à la génération des messages en temps réel pour la sortie MIDI, ou à la construction des tableaux de variations utililisés par Csound. Chaque paramètre est affecté à une séquence au niveau du score et sera attribué, selon le contexte, à un canal MIDI ou aux instruments Csound invoqués par la séquence.

Pour tout objet sonore il est possible de spécifier quels paramètres sont pris en compte. Ainsi, certains objets ne doivent pas être transposés ou modulés même s'ils font partie d'une séquence au cours de laquelle ces paramètres sont globalement modifiés.

Remarque méthodologique

Les concepts succintement décrits ci-dessus ont été progressivement introduits pour répondre à la demande des musiciens qui souhaitent disposer d'un environnement aussi flexible que possible pour la composition à partir de règles (Bel & Kippen 1992; Kippen & Bel 1992; Bel 1992b). Les étapes méthodologiques peuvent être résumées ainsi:

1. Les grammaires formelles se prêtent mal à la description de superpositions de séquences, d'où l'intérêt de la représentation polymétrique;
2. Dans une expression polymétrique il n'est pas intéressant d'expliciter toutes les relations de précédence temporelle. On doit donc permettre des représentations incomplètes qui peuvent être traitées par l'algorithme d'expansion polymétrique;
3. Une variante très proche de l'algorithme d'expansion polymétrique permet d'utiliser la period notation pour la représentation de séquences structurées par des "temps" de durées symboliques égales. On dispose alors d'un outil très simple de représentation de variations de durées;
4. On complète la period notation (déclarations de durées) par l'outil _tempo(x) qui déclare des vitesses;
5. La construction d'un diagramme de phases intégrant les fonctions décrites précédemment n'est possible pratiquement que si l'on permet la quantification et si celle-ci peut s'effectuer au niveau symbolique, ce qui justifie a posteriori les étapes précédentes.

Le prochain développement de l'algorithme d'expansion polymétrique portera sur l'interpolation des valeurs de tempo, permettant de gérer au niveau syntaxique des accélérations et des ralentissements et de s'affranchir pour cela des time-patterns difficiles à programmer.

Proposition d'une interface MBROLA pour BP2

L'idée de cette interface s'apparente à celle de l'interface Csound implémentée en 1995 dans le logiciel Bol Processor BP2 qui sert de support à mes activités de recherche en musicologie computationnelle. (Une présentation "grand-public" de BP2, avec téléchargement, se trouve sur <http://www.bp2.org>.) L'environnement de tâches MIDI/Csound est présenté succintement en annexe (voir Interaction between BP2, MIDI and Csound).

Pour l'interfaçage avec Csound, j'ai été amené à implémenter des structures de données d'un niveau d'abstraction suffisant pour couvrir aussi bien la représentation du temps sous MIDI (basée sur des points temporels) et sous Csound (basée sur des intervalles temporels). Il a fallu par ailleurs dégager des formalismes assez généraux pour les paramètres de contrôle qui ne se limitent plus aux grandeurs conventionnelles de MIDI (pitchbend, modulation...). Il a fallu enfin se dégager du système de 16 canaux MIDI pour travailler sur un nombre arbitraire d'instruments Csound.

L'interface Csound comprend un gestionnaire de description simplifiée des instruments Csound. Cette description ne contient pas les algorithmes de génération, mais elle permet de spécifier les emplacements et formats des arguments passés aux fonctions de chaque instrument. Il est nécessaire, par exemple, que BP2 effectue un mapping automatique si l'argument contient une grandeur fréquence en Hz alors que la syntaxe musicale est basée sur des cents ou des valeurs conventionnelles MIDI du pitchbend.

L'interfaçage de BP2 vers un autre système de production sonore, comme MBROLA, tirerait parti du travail effectué précédemment avec Csound. Le travail initial consisterait à s'assurer que les règles phonotactiques peuvent être énoncées dans le modèle grammatical de BP2, quitte évidemment à étendre ce modèle. On devrait enfin définir des performance controls spécifiques à la parole.

(A compléter... Commentaires bienvenus!)

Références

Bel, Bernard, 1990a

Time in Musical Structures. Interface, 19, 2-3, pp.107-135.

1990b
Acquisition et représentation de connaissances en musique. PhD dissertation, Faculté des Sciences de St Jérôme, Université Marseille III.

1992a
Symbolic and sonic representations of sound-object structures. In M. Balaban, K. Ebcioglu, and O. Laske (eds.) Understanding Music With AI. Menlo Park: AAAI Press, pp.64-109.

1992b
Modelling improvisational and compositional processes. Languages of Design, 1, pp.11-26.

1996
A flexible environment for music composition in non-European contexts. Journées d'Informatique Musicale (JIM 96), Caen (France), 1996. (Available with sound examples on <http://www.lpl.univ-aix.fr/~belbernard/music/jim96/jim96.htm>)

1998
Migrating Musical Concepts -- an Overview of the Bol Processor. Computer Music Journal, 22, 2, pp.56-64.

Bel, Bernard & Jim Kippen, 1992

Bol Processor grammars. In M. Balaban, K. Ebcioglu, and O. Laske (eds.), Understanding Music With AI. Menlo Park: AAAI Press, pp.366-400.

Kippen, Jim & Bernard Bel, 1992

Modelling Music with Grammars: Formal Language Representation in the Bol Processor. In A. Marsden and A. Pople (eds.), Computer Representations and Models in Music. London: Academic Press, pp.207-238.

Annexes

Structures polymétriques

Exemple élémentaire: on souhaite superposer deux séquences d'objets sonores: "a b c d e" et "f g h". Dans la syntaxe de BP2, cette superposition est simplement notée à l'aide d'une expression polymétrique::

{a b c d e, f g h}

BP2 calcule les durées symboliques (relatives) de chaque objet 'a', 'b'... et superpose les séquences de la manière suivante:

a _ _ b _ _ c _ _ d _ _ e _ _

f _ _ _ _ g _ _ _ _ h _ _ _ _

(diagramme de phases)

qui correspond à ce que l'on pouvait attendre intuitivement: "trois dans cinq". (Le symbole '_' indique la prolongation de durée de l'objet qui le précède.) L'expression polymétrique complète inférée (sur la base d'une complexité minimale du résultat) serait notée:

{a _ _ b _ _ c _ _ d _ _ e _ _, f _ _ _ _ g _ _ _ _ h _ _ _ _}

Period notation

Consider the sequence

C5.D5.G5.F5 G5.C5 D5.D#5.D5.C5 A#4.C5

in which "C5", "D5", etc. are sound-objects (here indicating notes in English score notation). Periods are used to separate beats. Symbolic durations will be resized automatically so that the sum of durations remains constant over each beat. In Western terminology, the resulting item would be said to contain crotchets and quavers. In Indian terminology, the same would be described as tempo changes from hargun (speed 1) to dogun (speed 2).

Changes of tempo may introduce fractional ratios. For instance,

C5 D5.G5 F5.G5 C5 D5.D#5 D5 C5.A#4 C5

Here, the duration of each note in "G5 C5 D5" and "D#5 D5 C5" is 2/3d that of the first note "C5". The explicit notation would be the following:

_tempo(3) C5_ _.D5_ _.G5_ _.F5_ _.G5_ C5._ D5_.D#5_ D5._ C5_.A#4_ _.C5_ _

in which '_' indicates a prolongation of the preceding note. The initial part "_tempo(3) C5_ _" means that the tempo is "speed 3" (tigun in Indian notation), but since "C5" is followed by two prolongation symbols its resulting duration (3/3 = 1) is the same as in the preceding example.

Time-patterns

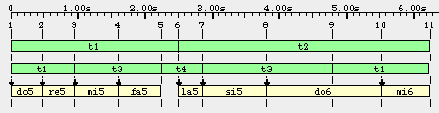
In smooth time (no pulse), it is possible to define time-patterns (arbitrary physical time ratios) creating a particular time structure. Time-patterns are constructed with the aid of time-objects conventionally notated 't1', 't2', etc. These may be combined with sequences of sound-objects in polymetric structures to generate a set of time streaks. The figure below shows a musical piece notated

do5 re5 mi5 fa5 - la5 si5 do6_ mi6

(in which '_' is a silence and '_' is the prolongation of do6) and constrained to a structure of time-patterns (a join-semilattice of time-span intervals). Time streaks are numbered 1 to 11.

"t1", "t2", etc. are time-objects, somehow similar to sound-objects except that they do not contain any sound-generating code. Here the piece is divided in two sections, namely "t1" and "t2", each of them lasting five beats with different physical durations. Let us assume that "t1" is a "normal duration" yielding five beats in 2.5 seconds, therefore we will set the metronome to 120 beats per minute. However, here the metronome does not construct a regular pattern of time streaks. It only serves as a time reference. This case is referred as measured smooth time. The second section "t2" is also five beats but it lasts 3.75 seconds, i.e. 1.5 times the first section. When specifying time-patterns each duration is written as an integer ratio:

t1 = 1/1
t2 = 3/2

This statement contains three pieces of information: (1) t2 is 1.5 times longer than t1, (2) the default duration of t1 is one metronome beat, (3) the default duration of t2 is 3/2 metronome beats. Indeed, (3) may be deducted from (1) and (2).

Let us now look at subdivisions. "t1" contains three subdivisions labelled "t1", "t3" and "t4". The new occurrence of "t1" has been resized so that the three subdivisions fit exactly in the first section. Only ratios are important at this stage. The picture shows that t3 is 1.33 times longer than t1, and t4 is two times shorter. Therefore,

t3 = 4/3
t4 = 1/2

The second section is subdivided as "t3" and "t1" in which the ratio between t3 and t1 is 1.33 as expected.

So far we have been able to define the hierarchy of time-span intervals as a tree structure. Let us now look at the note sequence itself. Time-object "t1" is subdivided as "do5" and "re5" with equal durations because all sound-objects have identical time references -- corresponding to ratio 1/1. "t3" is subdivided in a similar way, as well as "t4" which contains '-' (a silence) and "la5". The last part "t3 t1" is an interesting case since the time-span of "do6" is partly a subdivision of "t3" and of "t1". This indicates that the hierarchy of time-span intervals is not always a tree structure. Technically, it is called a join-semilattice.

Programming time-patterns in a grammar

A grammar producing the item shown above may be written as follows:

It is important that time-patterns appear in the leftmost fields of polymetric expressions. Here, "t1 t3 t4" and "t3 t1" are the first fields of polymetric expressions, whereas "t1 t2" is the second field because duration "10" should always be the first field. Suppose for instance that the second rule is changed to:

Part1 --> {do5 re5 mi5 fa5 - la5, t1 t3 t4}

This would yield:

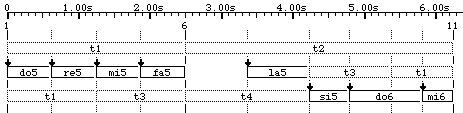
An incorrect use of time-patterns t1, t3, t4

in which duration ratios in section "t1 t3 t4" have been mistakenly determined by "do5", "re5",... "la5". In addition, symbolic durations are incorrect because Part1 now counts six units (do5, re5,...) instead of three (t1, t3, t4). Consequently, the symbolic duration of the entire item is 6 + 2 = 8 instead of 3 + 2 = 5.

Stepwise control of articulation

Instructions '_staccato()' and '_legato()' are used to modify the durations of sound-objects (articulation). "_staccato(x)" reduces the time-span of the next sound-object by x % of its duration, whereas "_legato(x)" increases it by x %. Thus, "_staccato(x)" is equivalent to "_legato(-x)".

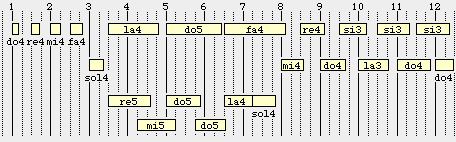
The following example illustrates the interpolation of articulation controls throughout a polymetric structure. The piece starts with "_staccato(80)" (only 20% duration left) and ends up with "_legato(100)" (100% dilation, except for the last sound-object 'do4'). The second field of the polymetric structure "re5 mi5 do5 do5 la4 sol4" varies independently from "_legato(60)" down to "_staccato(40)".

/2 _articulstep _staccato(80) do4 re4 mi4 fa4 sol4 {la4_ _ do5_ _ fa4_ _ , _legato(60) re5 mi5 do5 do5 la4 sol4 _staccato(40)} mi4 re4 do4 si3 la3 si3 _legato(100) do4 si3 do4

The resulting graphic score (on the physical time axis) will be:

Interaction between BP2, MIDI and Csound

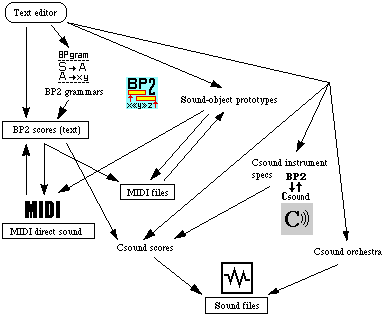The interaction between Bol Processor BP2, MIDI and Csound. BP2 scores in text format may be typed in, produced by a grammar or entered from a MIDI device. These scores contain simple notes, sound-objects and performance controls. A BP2 score combined with sound-object prototypes works out a direct MIDI output. The same output can be saved to MIDI files which may in turn be exported to sound-object prototypes. The BP2 score combined with a formal description of Csound instruments yields a Csound score. Csound is then invoked to produce a sound file using the orchestra file and the Csound score. (Bel 1998)