Se trata de uno de los primeros autómatas celulares construidos y es sin lugar a dudas el más conocido y estudiado de todos ellos. Se trata de un automáta celular binario (i.e las células toman sólo los valores 0 ó muerta y 1 ó viva), bidimensional con entornos de Moore. La actualización de la célula central puede realizarse mediante muchas familias de reglas; la cantidad de variantes que se ha introducido es muy extensa.

     El juego de la vida clásico se trata de las reglas originales introducidas por John Horton Comway en Scientific American en octubre de 1970. La idea consiste en modelar una situación en la cual ocurrieran las siguientes condiciones:

• No debe existir ninguna configuración inicial a partir de la cual se pueda probar de modo simple que la población crece sin control.
• Deben existir configuraciones iniciales que aparentemente provoquen un crecimiento descontrolado.
• Deben existir configuraciones iniciales simples que crecen y cambian durante un periodo considerable de tiempo para llegar a uno de los siguientes estados:
1. Desaparición completa (por superpoblación).
2. Situación estacionaria.
3. Configuración cíclica estable formada por dos o más estados que se van repitiendo.

     Con este motivo, Conway propuso las siguientes reglas:

• Una célula muerta vuelve a la vida si exactamente tres de sus vecinas están vivas. En otro caso permanece muerta.
• Una célula viva muere si no hay un mínimo de dos y un máximo de tres células vivas en su entorno. En otro caso permanece muerta.

     A pesar de que las reglas parecen y de hecho son realmente simples, se pueden establecer numerosos ejemplos de estructuras interesantes a partir de ellas.

Ejemplo:

     El juego de la vida tiende a evitar estructuras compactas, que denotarían superpoblación. En su lugar hacen su aparición otras estructuras más estables, que a ojos del espectador resultan "huecas". Como ejemplo, veamos lo que le ocurre a un bloque compacto:

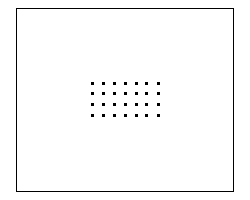Estado Inicial	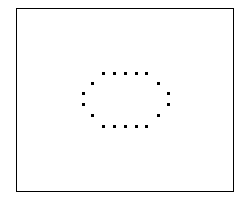Primera Iteración
Segunda Iteración	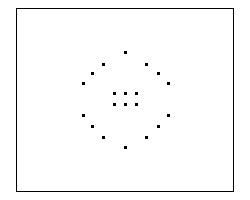Tercera Iteración
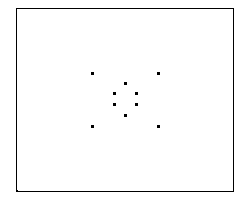Cuarta Iteración	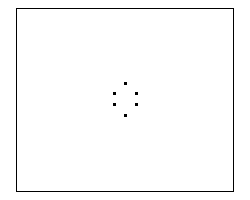Quinta Iteración (Estado Final)

Algunas estructuras del juego de la vida

     Desde que fué propuesto hace más de veinticinco años, el juego de la vida clásico ha generado un sinfín de bibliografía y estudios. Como consecuencia de esto, se han identificado numerosas estructuras peculiares. Expondremos aquí algunas de las más importantes y cómo se generan:

Como notación, * denota una célula viva, y un espacio denota una célula muerta.

Expresaremos la dinámica con flechas:

• Blinkers: Estructura oscilante con dos periodos.

*                 *
*  -->  ***  -->  *
*                 *

• Glider: Se trata de una estructura que sigue un ciclo, moviéndose una celda diagonalmente cada vez que lo completa.

 *
  *  -->  * *  -->    *  -->  *    -->   *
***        **       * *        **         *
           *         **       **        ***

• Spaceship: Un número finito de celdas que después de varias generaciones vuelve a aparecer con idéntica configuración en otro punto de la pantalla. Esto causa el efecto a ojos del espectador de una nave que se mueve, de ahí el nombre

   *
 *   *
*
*    *
*****

• Glider gun: Se trata de una estructura oscilante que emite Gliders periódicamente. El descubrimiento de la Glider gun probó la falsedad de una de las conjeturas básicas de conway, que ninguna población finita podría crecer sin límite.

                         *
                      ****    *
             *       ****     *
            * *      *  *         **
           *   **    ****         **
**         *   **     ****
**         *   **        *
            * *
             *

• Celdas unidad: Las celdas unidad se definen como "una estructura cuyo estado depende de su estado anterior y el estado anterior de sus vecinos, usando exactamente las reglas empleadas para calcularla: es decir, simula su propio universo". David Bell ha creado una que requiere 5760 generaciones para realizar una generación propia; se continúa buscando ejemplos más simples.

• Otras estructuras: Existen numerosas estructuras curiosas en el juego de la vida, bien por su estabilidad, propiedades especiales o incluso por su belleza. Por ejemplo un pentomino es una estructura consistente en cinco celdas que rápidamente decae a un estado estable; hay un pentomino especial (r-pentomino) que a diferencia de los demás se mantiene oscilando durante más de cuatrocientas iteraciones sin alcanzar un estado estable. Otro ejemplo interesante es la letra H : desaparece rápidamente, pero si movemos el marcador central a la casilla superior (es decir, formamos P) pasarán 173 generaciones antes de que se alcance un estado estable.

r-pantonimo

 **
**
 *


H:

* *        * *       ** **        ** **         *   *
***  -->  ** **  ->  ** **  -->  *     *  -->  *     *
* *        * *       ** **        ** **         *   *


Pi:

***
* *
* *