Pasaremos ahora a describir algunos procesos de construcción de fractales mediante los autómatas celulares. La filosofía de esta aproximación es la misma que siempre: reglas simples locales para generar comportamientos complicados globales.

     Es preciso notar una diferencia con otros métodos de construcción de estructuras autosemejantes, como por ejemplo los sistemas de funciones iteradas: en este caso, incluso desde el punto de vista teórico sólo podemos llegar a una aproximación del fractal, puesto que el conjunto de puntos que podemos representar es a lo sumo numerable.

     Esta objeción es puramente teórica, puesto que en la práctica tampoco podemos iterar infinitas veces un SFI y aunque fuesemos capaces de hacerlo la resolución de la pantalla (número de pixels) o de cualquier otro medio que empleemos para representar un fractal es finita. Sin embargo en la práctica esto fuerza a que debamos fijar a priori el grado de precisión que queremos, para fijar el tamaño del espacio celular: no podemos iterar hasta obtener una aproximación que consideremos "buena" como en SFI.

Ejemplo 1

     Consideremos las siguientes reglas (entornos de Moore):

• Una célula nace o permanece viva si exactamente una de las tres células de la fila inferior está viva. En otro caso muere.
• Si la célula se encuentra en el borde inferior del espacio celular, permanece viva indefinidamente.

     Así pues, partiendo del siguiente estado inicial:

     Vamos obteniendo...

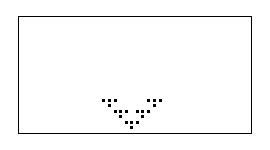
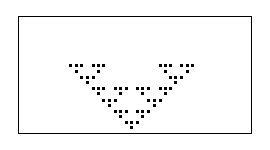
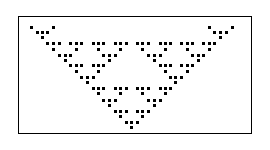
     Realizando un número mayor de iteraciones, con un espacio celular más grande, obtenemos:

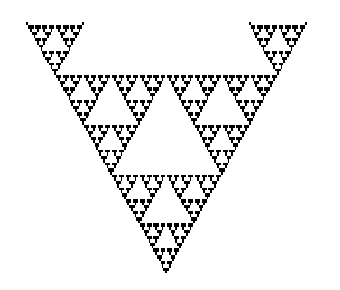
Ejemplo 2

     Consideraremos ahora entornos de von Neumann (regla N S E O) y una regla muy similar a la "one out of eight":

• Una célula viva permanece viva indefinidamente.
• Si una célula muerta tiene a su alrededor (i.e encima, debajo, a la derecha y a la izquierda) exactamente una célula viva la célula vuelve a la vida.

     Resulta interesante ver que en este caso, a diferencia del anterior, el proceso de formación no va creando estructuras semejantes entre sí, sino que consiste en un proceso de expansión-consolidación:

• En primera instancia el sistema se expande en todas las direcciones posibles (cuatro si se comienza con una celda central, tres con una celda en el borde), hasta que las ramas empiezan a acercarse.
• Posteriormente las ramas se acercan progresivamente entre sí hasta que se forma una estructura de tipo rombo, muy compacta. Dicho rombo empieza a expandirse por sus cuatro vértices y volvemos a la fase anterior.

     Para ver esto lo mejor es mostrar un ejemplo partiendo de una única celda central:

Estado Inicial	Tercera iteración y fin de la expansión
Cuarta iteración y consolidación	Quinta iteración
Sexta iteración; nueva expansión

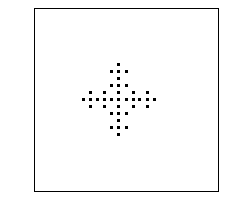     Ejemplo tras numerosas iteraciones en un espacio celular mucho mayor:

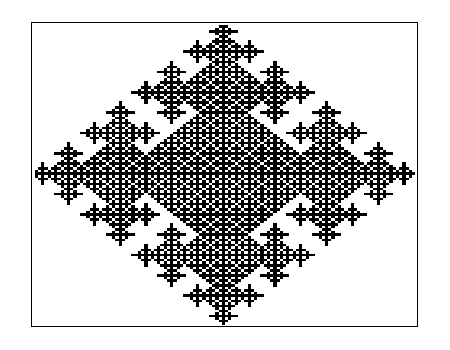
Ejemplo 2: Variantes

     Si en vez de considerar como entorno las cuatro casillas N S E O consideramos las diagonales, tenemos una estructura análoga que en algunas iteraciones se parece al copo de nieve matemático, si bien en el fondo es muy distinto:

Estado Inicial

Tras 11 iteraciones

     Las propiedades de crecimiento (expansión-consolidación) son análogas. Por otro lado, si consideramos un autómata celular probabilístico, que opte por utilizar en cada entorno las reglas de 2 (N S E O) y su variante (las diagonales) con probabilidad 1/2 el resultado no es ninguna estructura reconocible con propiedades elementales de autosemejanza:

Estado Inicial

Tras varias iteraciones

     De hecho puede verse que no se estabiliza aún después de muchas iteraciones.