 |
Chapter 10:Where Lies the Physics of the Mind?
|
Animal Consciousness?
Before leaving the topic of the importance of verbalization to consciousness,I should address the question,raised briefly earlier,of whether non-human animals can be conscious.It seems to me that people sometimes rely on animals' inability to speak as an argument against their having any appreciable consciousness - and,by implication,against their having any "rights". The reader may well perceive that I regard this as an untenable line of argument,since much sophisticated conscious thinking (eg mathematical) can be carried out without verbalization.The right side of the brain,also,is sometimes argued as having as "little" consciousness as a chimpanzee,also because of the lack of verbal ability (cf.LeDoux 1985,pp 197-216).
There is considerable controversy about whether chimpanzees and gorillas are,in fact, capable of genuine verbalization when they are allowed to use sign language [Ref: New Scientist 4May96 p22 {bonobo Kanzi} ;New Scientist 5Jun93 p36 R.Dawkins "Meet my cousin,the chimpanzee"] rather than speak in the normal human way (which they cannot do owing to the lack of suitable vocal chords.See various articles in Blakemore and Greenfield 1987.) It seems clear,despite the controversy,that they are able to communicate at least to a certain elementary degree by such means.In my own opinion,it is a little churlish of some people not to allow this to be called "verbalization". Perhaps,by denying apes entry to the verbalizers club,some would hope to exclude them from the club of conscious beings!
Leaving aside the question of speech,there is good evidence that chimpanzees are capable of genuine inspiration.Konrad Lorenz (1972) describes a chimpanzee in a room which contains a banana suspended from the ceiling just out of reach,and a box elsewhere in the room:
The matter gave him no peace,and he returned to it again and again.Then,suddenly - and there is no other way to describe it - his previously gloomy face "lit up".His eyes now moved from the banana to the empty space beneath it on the ground,from this to the box,then back to the space,and from there to the banana.The next moment he gave a cry of joy,and somersaulted over to the box in sheer high spirits.Completely assured of his success,he pushed the box below the banana.No man watching him could doubt the existence of a genuine "Aha" experience in anthropoid apes.
Note that,just as with Poincaré's experience as he boarded the omnibus,the chimpanzee was "completely assured of his success" before he had verified his idea.If I am right that such judgements require consciousness,then there is evidence here,also,that non-human animals can indeed be conscious.
An interesting question arises in connection with dolphins (and whales)[Ref: New Scientist 4May96 p20 "Zombies,Dolphins & Blindsight"].It may be noted that the cerebra of dolphins are as large (or larger) than our own,and dolphins can also send extremely complex sound signals to one another.It may well be that their large cerebra are needed for some purpose [porpoise?-LB :-)] other than "intelligence" on a human or near-human scale.Moreover,owing to their lack of prehensile hands,they are not able to construct a "civilization" of the kind we can appreciate - and,although they cannot write books for the same reason,they might sometimes be philosophers and ponder over the meaning of life and why they are "there"! Might they sometimes transmit their feelings of "awareness" via their complex underwater sound signals? I am not cognizant of any research indicating whether they use one particular side of their brains to "verbalize" and communicate with one another.In relation to the "split-brain" operations that have been performed on humans,with their puzzling implications of the continuity of "self" [Ref : D.Zohar "The Quantum Self" p36 -Other living things],it should be remarked that dolphins do not go to sleep with their whole brain simultaneously,but one side of the brain goes to sleep at a time.It would be instructive for us if we cold ask them how they feel about the continuity of consciousness!
Tilings and Quasicrystals
I now turn away from the sweeping speculations of the last few sections,and consider instead an issue that,though still somewhat speculative,is much more scientific and "tangible".At first this issue will appear to be an irrelevant digression.But the significance of it for us will become apparent in the next section.
Recall the tiling patterns depicted in Fig4.12,p.178.These patterns are somewhat remarkable in that they "almost" violate a standard mathematical theorem concerning crystal lattices.
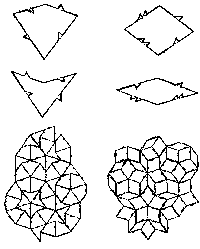
Fig 4.12
The theorem states that the only rotational symmetries that are allowed for crystalline patterns are twofold,threefold,fourfold and sixfold.By a crystalline pattern,I mean a discrete system of points which has translational symmetry ;that is,there is a way of sliding the pattern over itself ( i.e. is unchanged by that particular motion) and therefore has a period parallelogram (cf.Fig 4.8).
Fig 4.8
Examples of these tiling patterns with these allowed rotational symmetries are given in Fig 10.2.Now the patterns of Fig 4.12,like that depicted in Fig 10.3 (which is essentially the tiling produced by fitting together the tiles of Fig 4.11,p.177),on the other hand,almost have translational symmetry and they almost have fivefold symmetry-
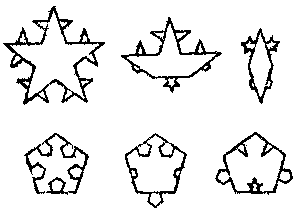
Fig 4.11
where "almost" means that one can find such motions of the pattern (translational and rotational,respectively) for which the pattern goes into itself to any desired pre-assigned degree of agreement just short of 100 per cent.There is no need to worry about the precise meaning of this here.The only point that will be of relevance for us is that if one had a substance in which the atoms were arranged at the vertices of the pattern,then it would appear to be crystalline,yet it would exhibit a forbidden fivefold symmetry!
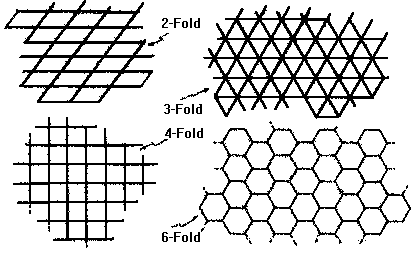
Fig 10.2
Periodic tilings with various symmetries (where the centre of the symmetry,in each case,is taken to be the centre of the tile).

Fig 10.3
A quasi-periodic tiling (essentially that which is produced by fitting together the tiles of Fig 4.11) with a crystallographically "impossible" fivefold quasi-symmetry.
In December 1984,the Israeli physicist Dany Shecthman who had been working with colleagues at the National Bureau in Washington DC, USA,announced the discovery of a phase of aluminium-manganese alloy which seemed indeed to be a crystalline-like substance- now referred to as a quasicrystal -with fivefold symmetry,In fact this quasicrystalline substance also exhibited a symmetry in three dimensions,and not only in the plane - giving a forbidden icosahedral symmetry in all (Shecthman et al.1984).(Three-dimensional "icosahedral" analogues of my fivefold plane tilings had been found by Robert Ammann in 1975,see Gardner 1989.) Shecthman's alloys formed only tiny microscopic quasicrystals,about 10-3 of a millimetre across,but later other quasicrystalline substances were found and,in particular,an aluminium - lithium - copper alloy for which the icosahedrally symmetric units can grow to about a millimetre in size,and are quite visible to the naked eye (see Fig 10.4).

Fig 10.4
A quasicrystal (an Al - Li -Cu alloy) with apparently impossible crystal symmetry.(From Gayle 1987.)
Now a remarkable feature of the quasicrystalline tiling patterns that I have been describing is that their assembly is necessarily non-local.That is to say,in assembling the patterns,it is necessary,from time to time,to examine the state of the pattern many,many "atoms" away from the point of assembly,if one is to be sure of not making an error when putting the pieces together.(This is perhaps akin to the apparently "intelligent groping" that I referred to in relation to natural selection.) This kind of feature is an ingredient of a considerable controversy that surrounds the question of quasicrystal structure and growth at the present time,and it would be unwise to attempt to draw definite conclusions until some of the outstanding issues are resolved.Nevertheless,one may speculate;and I shall venture my own opinion.First,I believe that some of these quasicrystalline substances are indeed highly organized,and their atomic arrangements are rather close in structure to the tiling patterns that I have been considering.Second,I am of the (more tentative) opinion that this implies that their assembly cannot reasonably be achieved by the local adding of atoms one at a time,in accordance with the classical picture of crystal growth,but instead there must be a non-local essentially quantum mechanical ingredient to their assembly.
[Even the growth of some actual crystals would involve similar problems,for example, where the basic unit cell involves several hundred atoms,as in what are called Frank - Casper phases.It should be mentioned,on the other hand,that a theoretical "almost local" (though still not local) growth procedure for fivefold symmetric quasicrystals has been suggested by Onoda,Steinhardt,DiVincenzo and Socolar (1988).]
The way that I picture this growth as taking place is that,instead of having atoms coming individually and attaching themselves at a continually moving growth line (classical crystal growth),one must consider an evolving quantum linear superposition of many different alternative arrangements of attaching atoms (by the quantum procedure U).Indeed,this is what quantum mechanics tells us must (almost always) be occurring! There is not one thing that happens;many alternative atomic arrangements must coexist in complex linear superposition.A few of these superposed alternatives will grow to very much bigger conglomerations and,at a certain point,the difference between the gravitational fields of some of the alternatives will reach the one-graviton level (or whatever is appropriate;see Ch8, p.475 "When does the state vector reduce?").At this stage one of the alternative arrangements - or,more likely,still a superposition,but a somewhat reduced superposition - will become singled out as the "actual" arrangement (quantum procedure R).This superposed assembly,together with reductions to more definite arrangements,would continue at a larger and larger scale until a reasonable-sized quasicrystal is formed.
Normally,when Nature seeks out a crystalline configuration,she is searching for a configuration of lowest energy (taking the background temperature to be zero).I am envisaging a similar thing with quasicrystal growth,the difference being that the state of lowest energy is much more difficult to find,and the "best" arrangement of atoms cannot be discovered simply by adding on atoms one at a time in the hope that each individual atom can get away with just solving its own minimizing problem.Instead,we have a global problem to solve.It must be a co-operative effort among a large number of atoms all at once [I am reminded of the story "Trillions"-LB]. Such co-operation,I am maintaining,must be achieved quantum-mechanically;and the way that is done is by many different combined arrangements of atoms being "tried" simultaneously in linear superposition (perhaps a little like the quantum computer (see also "Shadows" Ch 8 ) considered at the end of ch9.) The selection of a appropriate (though probably not best) solution to the minimizing problem must be achieved as the one graviton criterion(or appropriate alternative) is reached - which would presumably only occur when the physical conditions are just right.

