How Nature Does its Sums

If DNA is the building blocks of biology then maths maybe the builder,finds Simon Singh

It is very rare that I find myself standing in my local supermarket staring at the surface of a pineapple.But that is what happened soon after I heard Ian Stewart give a  lecture on the subject of his latest book. Stewart,who is one of Britain's most prominent mathematicians,has recently become interested in a new area of research at the frontier between biology and mathematics,which is already providing some startling insights into the living world......including pineapples.

Biomathematics is a reaction against the worship of DNA,and the opinion that genes govern all aspects of of life [Genetic Determinism -LB]. DNA is essentially a complex set of instructions,and in recent decades there has been a growing belief that it is this strand of molecules which guides all aspects of life.

A cross section through bamboo showing the arrangement of fibre bundles	Pine cones with two opposing spirals - nature exploiting maths	The seed head of a flower - such arrangements maximise the packing of seeds

However,if one looks at the instructions that would be required to dictate the nerve by nerve construction of the human nervous system, then it is clear that our DNA cannot carry enough information to complete this task,let alone all the others. Biomathematics claims that the information gap can be closed  by invoking mathematics and the laws of physics.

Physics and mathematics are capable of producing intricate patterns in non-organic constructions (for example, snowflakes and sand dunes). They can offer a range of patterns which will emerge spontaneously, given the correct starting conditions.The theory which is currently gaining support says that life operates by using DNA to create the right starting conditions,and thereafter physics and maths do all the rest,DNA is not the secret of life - hence the title of the book (Life's Other Secret: The New Mathematics of the Living World - Ian Stewart).

The strange case of the fascinating pineapple begins with the observation that its surface is covered in diamonds,which form two sets of spirals,twisting in opposite directions.There are 8 sloping to the left,and 13 sloping to the right.These numbers are special because they are part of the Fibonacci sequence (1,1,2,3,5,8,13,21,34,55...),in which the next number in the series is generated by adding the two previous numbers,ie 1+1=2 and 1+2=3,and so on.

Pattern by Numbers Seeds in a sunflower head are usually arranged in 34 clockwise and 55 anti- clockwise spirals

The sequence crops up in many other  plants,such as in the arrangement of seeds in the head of a sunflower which usually has 34 spirals going clockwise,and 55 going anti-clockwise.So far,this is just an observation,but biomathematics seeks to find an explanation.
An elegant argument in Ian Stewart's book explains that evolution encourages as many seeds as possible,physics provides the mechanism for packing them in most tightly,and mathematics leads to the Fibonacci sequence.

Stewart describes beautifully a whole series of of biological phenomena which can be elucidated by mathematics: the formation of the stomach in a frog embryo,the life cycle of the slime mould [Ref:Prof Bonner - Slime Moulds Cyclic AMP],the patterns on the skin of angel fish and tigers,the movement of bipeds,quadrupeds and hexapods,and animal behaviour.He does not have all the answers,but bear in mind that biomathematics is a recent development in science,and as compensation we get to see a subject full of controversy and youthful enthusiasm.

Finally,there may be people who suspect that the influence of mathematics can only serve to provide a more sterile view of life.This is not the case.The combination of DNA and mathematics enriches biology,and magnifies the wonder of life.Personally,I have found that my love of pineapples has grown enormously since learning about the mathematics of its surface.

Simon Singh is a television producer and author of "Fermat's Last Theorem" (Fourth Estate).

IS THE world a hopelessly untidy place? It all depends on your point of view of course. Biologists might see it as full of the rich diversity of nature. Physicists, perhaps view the world as containing an infinite array of phenomena to explore. To mathematicians, however, it is just a mess. For instance, they have struggled to use maths to describe something as apparently simple as the way insect populations vary from one season to the next. The problem is that one mathematical theorem describes how the adult population changes from day to day, while a totally different approach is needed to explain what happens over the long term, where numbers can change dramatically over different seasons. And you can't just bring these two bits of maths together to get an accurate picture. The problem plagues more than just studies of insect populations. Many phenomena, from combustion and stock markets to epidemics and crop harvests, present the same difficulty. 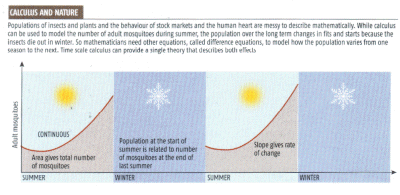Researchers simply have no way of predicting the behaviour of things that change smoothly at one level, but fitfully at another. But that might be about to change. In the past few years, a small group of mathematicians has developed a single mathematical theory that promises to revolutionise how we model real life. And nearly everywhere they look, they find another place to apply it. This promising idea goes by the unassuming name of time scale calculus. Outside mathematics, it is virtually unknown. Yet in the past couple of years it has emerged as a powerful and important tool whose obscurity belies its enormous potential. Take the work of mathematician Diana Thomas at Montclair State University in New Jersey. Thomas models populations of mosquitoes that carry West Nile virus, and time scale calculus, she believes, is the answer to all her problems. Suppose you count up the number of mosquitoes in a city every day. During the summer months, a steady stream of mosquito larvae mature into adults and then spend the next few weeks dodging predators such as birds and bats, and people trying to swat them. Plot the mosquito population against time through the summer and you could draw a smooth curve through the data without lifting your pencil off the page. Mathematicians call this continuous behaviour, and can almost always write down a mathematical formula to describe the shape of the curve. Such an equation is incredibly powerful. If you want to forecast the number of mosquitoes on any given day, for instance, you just plug the date into the formula and out pops the answer. And you can work out much more by calling on the theory of calculus devised by Newton and Leibniz. Suppose you want to know how many mosquitoes had infested the city so far that year. Calculus says you simply calculate the area under the curve. Meanwhile the slope of the curve tells you how fast the population is growing or shrinking from one moment to the next. That's all fine while life runs smoothly during the summer. But it is a different story for the rest of the year. In winter the adult mosquitoes die off completely so the curve drops to zero. The eggs lie dormant until the spring, when a new generation of mosquitoes emerges and the population rises again. So if you were plotting several years' worth of data, you would see a series of disconnected curves (see below). Researchers have developed a separate type of mathematics, called difference calculus, to deal with this "discrete", stop-start behaviour. Difference calculus gives you the equations to describe jumps. To see how difference equations work, think of your bank adding interest to your savings account at the end of each year. For 364 days your balance doesn't change, then it suddenly goes up. You can work out your new balance by adding a percentage of your savings to your last bank statement. The difference equation is simply the formula that gives the value of your savings at the start of the new year in terms of their value at the end of the last year. Similarly, you can relate the number of mosquitoes at the end of one season to the number at the start of the next season. Difference equations are not only useful in situations with discrete time jumps. When you have a messy problem to solve, it is often much easier to approximate it using difference equations rather than write down an exact continuous equation. And that's exactly what Thomas did in her work on mosquitoes carrying West Nile virus. Four years ago she started using difference equations to model the number of such mozzies in New York City. The virus, which lives mainly in birds, can be transmitted to humans, where it can cause a range of flu-like symptoms and, at worst, kill. Since West Nile arrived in New York in 1999 it has spread westwards in waves across the whole of North America. In an effort to control the mosquitoes in New York, public health officials spray insecticide throughout the city each summer. But so far, these efforts have largely failed. Tidy sums Thomas devised a difference equation that relates the mosquito population in any given week to the previous week's population, the birth rate, and the number of deaths due to both natural causes and spraying. She wrote down similar equations to describe the number of humans and birds infected with West Nile. Because the virus passes from one species to another, there is a complex interplay between all these equations. They have to take into account, for example, the probability that a mosquito picks up the virus from an infected bird and then goes on to bite a human. At first, Thomas's equations appeared to be successful. They modelled how mosquitoes catch West Nile from infected birds and then pass it on to other birds. And they predicted the impact of the infection on humans week by week. Better still, they successfully described both the active summer months and the winter months when West Nile lies dormant in female mosquitoes and larvae. Thomas's early models even indicated how often the authorities should spray New York to wipe out the virus. Public health officials seized upon the results and began spraying every two weeks, as Thomas's difference equations recommended. But the strategy didn't work: the virus continued to spread. The problem was that Thomas's model was just too simplistic. Although her equations could model certain aspects of the virus, they failed with others. West Nile doesn't stay strictly dormant in winter, as Thomas's difference equations assumed. As winter approaches and the mosquitoes in New York die, migrating birds carry the virus to warmer southern states, as well as Mexico and the Caribbean. Local mosquitoes catch West Nile from infected migrant birds and pass it on to healthy ones. So the virus spreads continually throughout the year, as more birds fall victim to it. Because Thomas's difference equations could not take account of such a continuous effect, they failed to correctly predict the number of infected birds returning to New York in the spring to start the cycle again in the north. To model West Nile properly, Thomas needed a way to model continuous and discrete processes at the same time: she needed calculus and difference equations lumped into one theorem. Unknown to her, a young mathematician had already done just that. In 1988, as a graduate student at the University of Augsburg in Germany, Stefan Hilger worked on some of the mathematical tools for modelling change. His adviser Bernd Aulbach asked Hilger if he could rewrite a theorem that worked for continuous variables so that it worked for discrete inputs too. When he looked closely at the two theorems, he found they weren't so different after all. As Hilger, now at the Catholic University of Eichstätt, Germany, played with other theorems and mathematical tools, he saw lots of similarities between the discrete and continuous versions. A pattern began to emerge, and it struck him that there was a deep connection between continuous calculus and difference equations. Instead of being two separate theories, they were really two strands of the same thing. From the emerging patterns, Hilger was able to devise a theory encapsulating them both. He found that when he plugged integers (...-2, -1,0.1.2..) -into his new theory the equations of difference calculus emerged the gaps betiveen the integers bring out discrete or stop-start behaviour from the theory. And when he fed in the full continuum of real numbers - integers and all the numbers in between. such as fractions and numbers like Ö2 - the theory took on the form of standard calculus. Since the set of real numbers is continuous, it brings out the continuous characteristics of calculus. Hilger had formulated nothing less than a grand unified theory for calculus. He called it time scale calculus - to mathematicians, "time scales" are simply different kinds of numbers: integers, or real numbers, for example. But while Hilger's colleagaes were impressed by the neatness of his theory, they couldn't see any practical use for it. So when his funding dried up 3 years later, time scale calculus seemed doomed to become a mathematical curio. Until 1997, that is. That's when German mathematician Martin Bohner came across time scale calculus by chance when he took up a position at the National University of Singapore. Until then he had been puzzled that regular calculus and difference equations could give amazingly similar results for certain problems, yet such different results for others. On the way from Singapore airport, a colleague, Ravi Agarwal, mentioned that time scale calculus might be the key. When Bohner read Hilger's thesis, he realised it was just what he needed. Together with Agarwal, he wrote five papers on time scale calculus in 6 months. The breakthrough was to realise that the time scale approach not only unites calculus and difference equations, it could also solve other problems that were a mix of stop-start and continuous behaviour. Over the next 5 years he threw himself into his research, reformulating many of the mathematical tricks of the trade so that they worked for time scale calculus. Mathematicians started to take notice of time scale calculus soon after Bohner wrote a book about it with Al Peterson at the University of Nebraska in Lincoln. Equations for the real world And it was Peterson who gave Thomas the breakthrough she needed in her own work. In 2000 she was at a conference in Rhode Island and heard him give a talk on time scale calculus. She realised that the new theory would help with a problem she was working on at the time with her colleague Michael Jones: modelling the healing of wounds. A few months later, when Thomas realised her West Nile virus difference equations were flawed, it dawned on her that time scale calculus might be able to rescue her West Nile model too. Because time scale calculus bridges the divide between the discrete and continuous aspects of West Nile, Thomas believes it could be the best way to understand and control the disease. The unified approach means that Thomas's sophisticated new models can take into account dozens of variables, including many that were previously ignored, such as the effect of temperature variations on the life cycle of mosquitoes. She eventually hopes to produce an intricate model of the virus's evolution in different areas. "Diana's model integrates all these different, complex processes into one," says Jessica Hartman, an epidemiologist at the New York City health department. "As far as I know it is truly unique in this respect:" Though the latest West Nile model is not yet fully developed, Thomas and Hartman believe that once it is complete it will provide real ammunition in the battle against the disease. By providing accurate forecasts of where future virus hot spots are likely to emerge, the pair hope the model will lead to more effective health-policy decisions. And this maybe just the beginning of real-life applications for time scale calculus. Joan Hoffacker and her colleagues at the University of Georgia in Athens in the US have used the theory to model how students suffering from the eating disorder bulimia are influenced by their college friends. With the new theory, they can model how the number of sufferers changes during the continuous college term as well as during long breaks. Hoffacker urges caution about premature judgements on the merits of time scale calculus, and admits, "We don't have an application that is finished yet:" However, she is pushing it further, and has teamed up with Billur Kaymakçalan, a mathematician at Georgia Southern University in Statesboro, to see if time scale theory could model electrical activity in the heart. You only have to look at a trace from an electrocardiogram to see that every heartbeat involves a huge spike in electrical activity followed by a period of calm. So far time scale calculus's main applications have been in biological systems. But it is about to spark a much wider revolution. Tom Gard, Hoffacker's colleague in Athens, has started looking at how the theory could improve models of the stock market, with its ever changing rises and falls punctuated by spectacular crashes and gains. Another enthusiast is Qin Sheng, a computer scientist at the University of Dayton in Ohio. He has found that he can make much more accurate simulations of combustion in engines based on time scale calculus. It allows him to model the dramatic spatial jumps in temperature that are so characteristic of burning fuels. Sheng's work shows that time scale calculus can be useful where the sudden changes in behaviour are spatial as well as temporal. Indeed, he predicts that anything where there is a boundary between large and small-scale behaviour, such as the interfaces of nanoscale structures embedded in other materials, will benefit from the new unified approach. "It will merge into mainstream scientific computation sooner or later," he predicts. It looks like that may happen sooner rather than later. Although time scale calculus is still rather obscure, things are changing fast. Last year the number of researchers citing one of Bohner's papers leapt dramatically, and the citations are now growing steadily. It seems time scale calculus is turning into something big, an indispensable tool for scientists interested in prediction. But who can tell? Invented in 1988, discarded 3 years later, and rediscovered in 1997, it now seems to be moving into a more stable phase. With such stop-start beginnings followed by continuous growth, what on earth could possibly model its behaviour? Oh, hang on... Vanessa Spedding is a science writer based in the UK. Additional reporting by Valerie Jamieson Further reading: Dynamic Equations an Time Scales by Martin Bohner and Allan C. Peterson (Birkhauser)

UNIVERSAL VEINS. Despite the stunning variety of leaf shapes from one plant variety to another, a universal formula may guide the vein patterns in all leaves. Researchers at the Laboratorie de Physique Statistique (S. Bohn, 33-1-4432-3447, [email protected]) and the Museum National d'Historie Naturalle, both in Paris, recently studied the networks of veins in leaves from several plant types. An analysis of leaf vein networks revealed simple relationships between the angles that veins form when they intersect and the thickness of the veins at the intersections. At a three-way junction of similarly sized veins, the angles between the veins are all roughly 120 degrees (see image at www.aip.org/mgr/png). At locations where a small vein joins a large vein, however, the angles between the small vein and the larger one approach 90 degrees. Imagine, for example, the angles formed by pulling on a light thread tied to a taut rope. The similarity between a network of threads and ropes exerting forces on each other and the patterns in leaf veins suggested to the researchers that there is an underlying mechanism in leaf formation that is reminiscent of simple mechanics problems. The model breaks with theories of leaf networks related to soap froths (which require all intersection angles to equal 120 degrees), crack propagation (with 90 degree intersections where new cracks meet old cracks), and Turing diffusion (which leads to patterns that resemble spreading tree branches, rather than the net-like patterns found in leaf veins). Some botanists had considered leaf veins as potential tools for categorizing plants. The universal similarity of vein structure from one plant to another suggests that the patterns provide insight to leaf mechanics, but are of little help in distinguishing or cataloging plants. (S. Bohn et al., Phys. Rev. E, June 2002; text at www.aip.org/physnews/select)

"There is not a fine tree producing rotten fruit;again there is not a rotten tree producing fine fruit. For each tree is known by its own fruit"
- Luke 6:43,44 -quoted in "What has religion done for mankind?"

"Even from the standpoint of the skeptic,a reasonable and candid search into the unknown,by the light of what is known,will guide the ubiased,intelligent reasoner in the direction of truth. Yet it is evident that without a direct revelation of the plans and purposes of God,men could only approximate the truth,and arrive at indefinite conclusions.But let us for the moment lay aside the Bible,and look at things from the standpoint of reason alone. He who can look into the sky with a telescope,or even with his natural eye alone,and see its symmetry,beauty,order,harmony and diversity,and yet doubt the Creator of these is vastly his superior both in wisdom and power,or who can suppose for a moment that such order came by chance,without a creator,has so far lost or ignored the faculty of reason as to be properly considered what the Bible terms him,a fool (one who ignores or lacks reason):"The fool hath said in his heart,There is no God." However it happened,at least that much of the Bible is true,as every reasonable mind must conclude;for it is a self evident truth that effects must be produced by competent causes.Every plant and every flower,even speaks volumes of testimony on this subject. Intricate in construction,exquisitely beautiful in form an texture,each speaks of wisdom and skill above human.How short sighted the absurdity which boasts of human skill and ingenuity,and attributes to mere chance the regularity,uniformity and harmony of nature;which acknowledges the laws of nature,while denying that nature has an intelligent Lawgiver." -"The Divine Plan of the Ages" [Ignorant nonsense-LB]

MAIN INDEX

REFERENCE GUIDE

TRANSCRIPTS

GLOSSARY