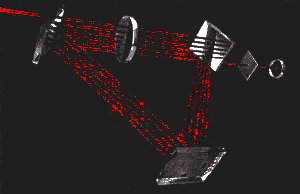
LASER BEAM following a spiralling path
that leads to a photon detector can illustrate the so-called quantum Zeno
effect, an element of interaction-free measurements.
Quantum optics demonstrates the existence of interaction-free measurements: the detection of objects without light-or anything else-ever hitting them
by Paul Kwiat, Harald Weinfurter and Anton Zeilinger
|
LASER BEAM following a spiralling path
that leads to a photon detector can illustrate the so-called quantum Zeno
effect, an element of interaction-free measurements. |
In Greek mythology, the hero Perseus is faced with the unenviable
task of fighting the dreaded Medusa. The snake-haired beast is so hideous
that a mere glimpse of her immediately turns any unlucky observer to stone.
In one version of the story, Perseus avoids this fate by cleverly using his
shield to reflect Medusa's image back to the creature herself, turning her
to stone. But what if Perseus did not have well-polished armour? He presumably
would have been doomed. If he closed eyes, he would have been unable to find
his target. And the smallest peek would have allowed some bit of light striking
Medusa to reflect into his eye, having thus "seen" the monster, he would
have been finished.
In the world of physics, this predicament might be summed up
by a seemingly innocuous, almost obvious claim made in 1962 by Nobelist Dennis
Gabor, who invented holography. Gabor asserted, in essence, that no observation
can be made with less than one photon-the basic particle, or quantum, of
light-striking the observed object.
In the past several years, however, physicists in the increasingly bizarre
field of quantum optics have learned that not only is this claim far from
obvious, it is, in fact, incorrect. For we now know how to determine the
presence of an object with essentially no photons having touched it.
Such
interaction-free
measurement seems to be a contradiction-if there is no interaction, how
can there be a measurement? That is a reasonable conundrum in classical
mechanics, the field of physics describing the motions of footballs, planets
and other objects that are not too small. But quantum mechanics- the science
of electrons, photons and other particles in the atomic realm-says otherwise.
Interaction-free measurements can indeed be achieved by quantum mechanics
and clever experimental designs. If Perseus had been armed with a knowledge
of quantum physics, he could have devised a way to "see" Medusa without any
light actually striking the Gorgon and entering his eye. He could have looked
without looking.
Such quantum prestidigitation offers many ideas for building
detection devices that could have use in the real world. Perhaps even more
interesting are the mind-boggling philosophical implications. Those applications
and implications are best understood at the level of thought experiments:
streamlined analyses that contain all the essential features of real experiments
but without the practical complications.
So, as a thought experiment, consider a variation of a shell
game, which employs two shells and a pebble hidden under one of them. The
pebble, however, is special: it will turn to dust if exposed to any light.
The player attempts to determine where the hidden pebble is but without exposing
it to light or disturbing it in any way. If the pebble turns to dust, the
player loses the game.
Initially, this task may seem impossible, but we quickly see that as long
as the player is willing to he successful half the time, then an easy strategy
is to lift the shell he hopes does not contain the pebble. If he is right,
then he knows the pebble lies under the other shell, even though he has not
seen it. Winning with this strategy, of course, amounts to nothing more than
a lucky guess.
Next, we take our modification one step further, seemingly
simplifying the game but in actuality making it impossible for a player limited
to the realm of classical physics to win. We have only one shell, and a random
chance that a pebble may or may not be under it. The player's goal is to
say if a pebble is present, again without exposing it to light.
Assume there is a pebble under the shell. If the player does not look under
the shell, then he gains no information. If he looks, then he knows the pebble
was there, except that he has necessarily exposed it to light and so finds
only a pile of dust. The player may try to dim the light so that there is
very little chance of it hitting the pebble. For the player to see the pebble,
however, at least one photon must have hit it, by definition, implying that
he has lost.
Elitzur, Vaidman and the Bomb
To make the game more dramatic, Avshalom C. Elitzur
and Lev Vaidman, two physicists at Tel Aviv University, considered the pebble
to be a "superbomb" that would explode if just a single photon hit it. The
problem then became: determine if a pebble bomb sits under a shell, but don't
set it off.
Elitzur and Vaidman were the first researchers to offer any solution to the
problem. Their answer works, at best, half the time. Nevertheless, it was
essential for demonstrating any hope at all of winning the game.
Their method exploits the fundamental nature of light. We have
already mentioned that light consists of photons, calling to mind a particle
like quality. But light can display distinctly wavelike characteristics-notably
a phenomenon called interference. Interference is the way two waves add up
with each other. For example, in the well-known double-slit experiment, light
is directed through two slits, one above the other, to a far away screen.
The screen then displays bright and dark fringes [see illustration below].
|
|
INTERFERENCE occurs when a laser is shone through two slits, which generate concentric light waves that interfere with each other (top left).The waves can add constructively or destructively (top right), yielding the characteristic interference pattern of bright and dark bands (bottom). |
|
|
|
The bright fringes correspond to places where the crests and
troughs of the light waves from one slit add constructively to the crests
and troughs of waves from the other slit. The dark bands correspond to
destructive interference, where the crests from one slit cancel the troughs
from the other. Another way of expressing this concept is to say that the
bright fringes correspond to areas on the screen that have a high probability
of photon hits, and the dark fringes to a low probability of hits.
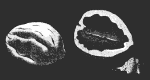 |
PHYSICIST'S SHELL GAME is a thought experiment that illustrates the potential of interaction-free measurements. A special pebble may be under a shell; if any light touches the pebble, it turns to dust. How can one determine which shell hides the pebble? |
According to the rules of quantum mechanics, interference Occurs
whenever there is more than one possible way for a given outcome to happen,
and the ways are not distinguishable by any means (this is a more general
definition of interference than is often given in textbooks). In the double-slit
experiment, light can reach the screen in two possible ways (from the upper
or the lower slit), and no effort is made to determine which photons pass
through which slit. If we somehow could determine which slit a photon passed
through, there would be no interference, and the photon could end up anywhere
on the screen. As a result, no fringe pattern would emerge. Simply put, without
two indistinguishable paths, interference cannot occur.
As the initial setup for their hypothetical measuring system,
Elitzur and Vaidman start with an interferometer-a device consisting of two
mirrors and two beam splitters. Light entering the interferometer hits a
beam splitter, which sends the light along two optical paths: an upper and
a lower one. The paths recombine at the second beam splitter, which sends
the light to one of two photon detectors [see illustration below]. Thus,
the interferometer gives each photon two possible paths between the light
source and a detector.
|
|
ELITZUR-VAIDMAN EXPERIMENT gives a photon a choice of two paths to follow. The optical elements are arranged (left) so that photons always go to detector D-light (corresponding to constructive interference, but never to D-dark (corresponding to destructive interference). The presence of a pebble in one path, however, occasionally sends a photon to D-dark (right), indicating that an interaction-free measurement has occurred. |
|
If the lengths of both paths through the interferometer
are adjusted to be exactly equal, the setup effectively becomes the double-slit
experiment. The main difference is that the photon detectors take the place
of the screen that shows bright and dark fringes. One detector is positioned
so that it will detect only the equivalent of the bright fringes of an
interference pattern (call that detector D- light). The other one records
the dark fringes-in other words, no photon ever reaches it (call that detector
D-dark).
Pebble in the Path
What happens if a pebble is placed into one of the paths, say, the upper
one ? Assuming that the first beam splitter acts randomly, then with 50 percent
likelihood, the photon takes the upper path, hits the pebble (or explodes
the superbomb) and never gets to the second beam splitter.
If the photon takes the lower path, it does not hit the pebble. Moreover,
interference no longer occurs at the second beam splitter, for the photon
has only one way to reach it. Therefore, the photon makes another random
choice at the second beam splitter. It may be reflected and hit detector
D-light; this outcome gives no information, because it would have happened
anyway if the pebble had not been there. But the photon may also go to detector
D-dark. If that occurs, we know with certainty that there was an object in
one path of the interferometer, for if there were not, detector D-dark could
not have fired. And because we sent only a single photon, and it showed up
at D-dark, it could not have touched the pebble. Somehow we have managed
to make an interaction-free measurement-we have determined the presence of
the pebble without interacting with it.
Although the scheme works only some of the time, we emphasise
here that when the scheme works, it works completely. The underlying
quantum-mechanical magic in this feat is that everything, including light,
has a dual nature-both particle and wave. When the interferometer is empty,
the light behaves as a wave. It can reach the detectors along both paths
simultaneously, which leads to interference. When the pebble is in place,
the light behaves as an indivisible particle and follows only one of the
paths. The mere presence of the pebble removes the possibility of interference.
even though the photon need not have interacted with it.
To demonstrate Elitzur and Vaidman's idea, we and Thomas Herzog,
now at the University of Geneva, performed a real version of their thought
experiment two years ago and thus demonstrated that interaction-free devices
can be built. The source of single photons was a special
nonlinear optical crystal. When
ultraviolet photons from a laser were directed through the crystal, sometimes
they were "down -
converted" into two daughter photons of lower energy that travelled off
at about 30 degrees from each other. By detecting one of these photons, we
were absolutely certain of the existence of its sister, which we then directed
into our experiment.
That photon went into an interferometer (for simplicity, we
used a slightly different type of interferometer than the one Elitzur and
Vaidman proposed). The mirrors and beam splitter were aligned so that nearly
all the photons left by the same way they came in (the analogue of going
to detector D-light in the Elitzur-Vaidman example or, in the double-slit
experiment, of going to a bright fringe). In the absence of the pebble, the
chance of a photon going to detector D-dark was very small because of destructive
interference (the analogue of the dark fringes in the double-slit experiment)
[see illustration below].
|
|
|
DEMONSTRATION of the Elitzur - Vaidman scheme uses light from a down-conversion crystal, which enters a beam splitter, bounces off two mirrors and interferes with itself back at the beam splitter (top). No light reaches D-dark (corresponding to destructive interference; constructive interference is in the direction from which the photon first came). If a mirror "pebble" is inserted into a light path, no interference occurs at the beam splitter; D-dark sometimes receives photons (left). |
But introducing a pebble into one of the pathways changed the
odds. The pebble was a small mirror that directed the light path to another
detector ( D-pebble). We then found that about half of the time, D-pebble
registered the photon, whereas about one fourth of the time D-dark did (the
rest of the time the photon left the interferometer the same way it came
in, giving no information). The firing of D-dark was the interaction-free
detection of the pebble.
In a simple extension of the scheme, we reduced the reflectivity of the beam
splitter, which lessened the chance that the photons would be reflected onto
the path containing the mirror to D-pebble. What we found, in agreement with
theoretical prediction, was that the probabilities of the photons going to
D-pebble and going to D-dark became more and more equal. That is, by using
a barely reflective beam splitter, up to half the measurements in the
Elitzur-Vaidman scheme can be made interaction-free ( instances in which
the photons leave the interferometer the same way they came in are not counted
as measurements).
The Quantum Zeno Effect
The question immediately arose: Is 50 percent the best we can do? Considerable,
often heated, argument ensued among us, for no design change that would improve
the odds was evident. In January 1994, however, Mark A. Kasevich of Stanford
University came to visit us at Innsbruck for a month, and during this stay
he put us on to a solution that, if realised, makes it possible to detect
objects in an interaction-free way almost every time. It was not the first
instance, and hopefully not the last, in which quantum optimism triumphed
over quantum pessimism.
The new technique is more or less an application of another
strange quantum phenomenon, first discussed in detail in 1977 by Baidyanath
Misra, now at the University of Brussels, and E. C. George Sudarshan of the
University of Texas at Austin. Basically, a quantum system can be trapped
in its initial state, even though it would evolve to some other state if
left on its own. The possibility arises because of the unusual effect that
measurements can have on quantum systems. The phenomenon is called the quantum
Zeno effect, because it resembles the famous paradox raised by the Greek
philosopher Zeno, who
denied the possibility of motion to an arrow in flight because it appears
"frozen" at each instant of its flight. It is also known as the watched-pot
effect, a reference to the aphorism about boiling water. We all know that
the mere act of watching the pot should not (and does not) have any effect
on the time it takes to boil the water. In quantum mechanics, however, such
an effect actually exists-the measurement affects the outcome (the principle
is called the projection postulate).
|
POLARISATION refers to the vibrations of light waves as they move through space. |
Kasevich essentially reinvented the simplest example of this effect, which was first devised in 1980 by Asher Peres of the Technion-Israel Institute of Technology. The example exploits yet another characteristic of light: polarisation. Polarisation is the direction in which light waves oscillate-up and down for vertically polarised light, side to side for horizontally polarised light. These oscillations are at right angles to the light's direction of propagation. Light from the sun and other typical sources generally vibrates in all directions, but here we are concerned mostly with vertical and horizontal polarisations. Consider a photon directed through a series of, say, six devices that each slightly rotates the polarisation of light so that a horizontally polarised photon ends up vertically polarised [see illustration below]. These rotators might be glass cells containing sugar water, for example. At the end of the journey through the rotators, the photon comes to a polariser, a device that transmits photons with one kind of polarisation but absorbs photons with perpendicular polarisation. In this thought experiment, the polariser transmits only horizontally polarised light to a detector.
|
QUANTUM ZENO EFFECT can be demonstrated with devices that rotate polarisation 15 degrees. After passing through six such rotators, the photon changes from a horizontal polarisation to a vertical one and so is absorbed by the polariser (top row). Interspersing a polariser after each rotator, however, keeps the polarisation from turning (bottom row). |
We will start with a photon horizontally polarised, and each
rotator will turn the polarisation by 15 degrees. It is clear, then, that
the photon will never get to the detector, for after passing through all
the cells, its polarisation will have turned 90 degrees ,15 degrees for each
of the six rotators so that it becomes vertical. The polariser absorbs the
photon. This stepwise rotation of the polarisation is the quantum evolution
that we wish to inhibit.
Interspersing a horizontal polariser between each polarisation
rotator does the trick. Here's why. After the first rotator, the light is
not too much turned from the horizontal. This means that the chance that
the photon is absorbed in the first horizontal polariser is quite small,
only 5.7 percent. (Mathematically, it is given by the square of the sine
of the turning angle.)
If the photon is not absorbed in the first polariser, it is again in a state
of horizontal polarisation - it must be, because that is the only possible
state for light that has passed a horizontal polariser. At the second rotator,
the polarisation is once again turned 15 degrees from the horizontal, and
at the second polariser, it has the same small chance of being absorbed;
otherwise, it is again transmitted in a state of horizontal polarisation.
The process repeats until the photon comes to the final polariser.
An incident photon has a two-thirds chance of being transmitted
through all six inserted polarisers and making it to the detector; the
probability is given by the relation (cos2(15
degrees))6 . Yet as we increase the number of stages, decreasing
the polarisation - rotation angle at each stage accordingly that is, 90 degrees
divided by the number of stages), the probability of transmitting the photon
increases. For 20 stages, the probability that the photon reaches the detector
is nearly 90 percent. If we could make a system with 2,500 stages, the
probability of the photon being absorbed by, one of the polarisers would
be just one in 1,000. And if it were possible to have an infinite number
of stages, the photo would always get through. Thus, we would have completely
inhibited the evolution of the rotation.
|
EXPERIMENTAL REALISATION of the quantum Zeno effect was accomplished by making the photon follow a spiral-stair- case path, so that it traversed the polarisation rotator six times. Inserting a polariser next to the rotator suppressed the rotation of the photon's polarisation. |
|
|
To realise the quantum Zeno effect, we used the same nonlinear
crystal as before to prepare a single photon. Instead of using six rotators
and six polarisers, we used just one of each; to achieve the same effect,
we forced the photon through them six times, employing three mirrors as a
kind of spiral staircase [see illustration above]. In the absence of the
polariser, the photon exiting the staircase is always found to be vertically
polarised. When the polariser is present, we found that the photon was
horizontally polarised (unless the polariser blocked it). These cases occurred
roughly two thirds of the time for our six-cycle experiment, as expected
from our thought-experiment analysis.
Next we set out to make an interaction-free measurement-that is, to detect an opaque object without any photos hitting it-in a highly efficient manner. We devised a system that was somewhat of a hybrid between the Zeno example and the original Elitzur-Vaidman method. A horizontally polarised photon is let into the system and makes a few cycles (say, six again) before leaving. (For this purpose, one needs a mirror that can be "switched" on and off very quickly; fortunately, such mirrors, which are actually switchable interference devices, have already been developed for pulsed lasers.) At one end of the system is a polarisation rotator, which turns the photon's polarisation by 15 degrees in each cycle. The other end contains a polarisation interferometer. It consists of a polarising beam splitter and two equal- length interferometer paths with mirrors at the ends [see illustration below].
|
EFFICIENT MEASUREMENTS that are interaction - free combine the setups of the quantum Zeno effect and the Elitzur-Vaidman scheme. The photon enters below the switchable mirror and follows the optical paths six times before being allowed to exit through the mirror. Its final polarisation will still be horizontal if there is a pebble in one light path; otherwise, it will have rotated to a vertical polarisation. |
At the polarising beam splitter, all horizontally polarised
light is transmitted, and all vertically polarised light is reflected; in
essence, the transmission and reflection choices are analogous to the two
paths in the double-slit experiment. In the absence of an object in the
polarisation interferometer, light is split at the beam splitter according
to its polarisation, reflects off the mirrors in each path and is recombined
by the beam splitter. As a result, the photon is in exactly the same state
as before it entered the interferometer (that is, with a polarisation turned
15 degrees toward the vertical). So, after six cycles, the polarisation ends
up rotated to vertical.
The situation changes when an opaque object is placed in the
vertical polarisation path of the interferometer. This situation is analogous
to having the six polarisers inserted in the quantum Zeno effect experiment.
So in the first cycle, the chance that the photon-the polarisation of which
has been turned only 15 degrees from horizontal-enters the vertical -
polarisation path (and is then absorbed by the object) is very small ( 6.7
percent, as in the Zeno thought experiment). If this absorption does not
happen, the photon must have entered the horizontal path instead, and its
polarisation is reset to be purely horizontal.
Just as in the Zeno example, the whole process repeats at each
cycle, until finally, after six cycles, the bottom mirror is switched off,
and the photon leaves the system. Measuring the photon's polarisation, we
find it still to be horizontal, implying that a blocker must reside in the
interferometer. Otherwise, the photon would have been vertically polarised
when it left. And by using more cycles, we can make the probability that
the photon is absorbed by the object as small as we like. Preliminary results
from new experiments at Los Alamos National Laboratory have demonstrated
that up to 70 percent of measurements could be interaction-free. We soon
hope to increase that figure to 85 percent.
Applying Quantum Magic
What good is all this quantum conjuring? We feel that the situation resembles
that of the early years of the laser, when scientists knew it to be an ideal
solution to many unknown problems. The new method of interaction-free measurement
could be used, for instance, as a rather unusual means of photography, in
which an object is imaged without being exposed to light.
The "photography" process would work in the following way: Instead of sending
in one photon, we would send in many photons, one per pixel, and perform
interaction-free measurements with them. In those regions where the object
did not block the light path of the interferometer, the horizontal polarisation
of the photons would undergo the expected stepwise rotation to vertical.
In those regions where the object blocked the light path, a few of the photons
would be absorbed; the rest would have their polarisations trapped in the
horizontal state. Finally, we would take a picture of the photons through
a polarising filter after they had made the requisite number of cycles.
If the filter were horizontally aligned, we would obtain an
image of the object; if vertically aligned, we would obtain the negative.
In any case, the picture is made by photons that have never touched the object.
These techniques can also work with a semitransparent object and may possibly
be generalised to find out an object's colour (although these goals would
be more difficult).
A variation of such imaging could someday conceivably prove valuable in
medicine-for instance, as a means to image living cells. Imagine being able
to x-ray someone without exposing them to many penetrating x-rays. Such imaging
would therefore pose less risk to patients than
standard x-rays. (Practically speaking, such x-ray photography is unlikely
to be realised, considering the difficulty of obtaining optical elements
for this wavelength of light.)
|
The Projection Postulate The postulate states that for any measurement made on a quantum system only certain answers are possible. Moreover, after the measurement, the quantum system is in a state determined by the obtained results. So a photon that has passed through a horizontal polariser is necessarily horizontally polarised, even if it were originally polarised at a nearly vertical angle (the polariser eliminates the vertical component of the polarisation). The probability of transmission in this case, though, would be low. |
A candidate for more immediate application is the imaging of
the clouds of ultracold atoms recently produced in various laboratories.
The coldest of these exhibit
Bose-Einstein condensation, a new
type of quantum state in which many atoms act collectively as one entity.
In such a cloud every atom is so cold-that is, moving so slowly-that a single
photon can knock an atom out of the cloud. Initially, no way existed to get
an image of the condensate without destroying the cloud. Interaction-free
measurement methods might be one way to image such a collection of atoms.
Besides imaging quantum objects, interaction-free procedures
could also make certain kinds of them. Namely, the techniques could extend
the creation of
"Schrödinger's cat,"
a much loved theoretical entity in quantum mechanics. The quantum feline
is prepared so that it exists in two states at once: it is both alive and
dead at the same time-a superposition of two states. Earlier this year workers
at the National Institute of Standards and Technology managed to create a
preliminary kind of "Schrödinger's cat" - a "kitten"- with a beryllium
ion. They used a combination of lasers and electromagnetic fields to make
the ion exist simultaneously in two places spaced 83 nanometers apart - a
vast distance on the quantum scale.
If such an ion were interrogated with the interaction-free methods,
the interrogating photon would also be placed in a superposition. It could
end up being horizontally and vertically polarised at the same time. In fact,
the kind of experimental setup discussed above should be able to place a
group of, say, 20 photons in the same superposition. Every photon would "know"
that it has the same polarisation as all the others, but none would know
its own polarisation. They would remain in this superposition until a measurement
revealed them to be all horizontally polarised or all vertically polarised.
The sizeable bunch of photons stuck in this peculiar condition would show
that quantum effects can be manifested at the macroscopic scale.
|
PHOTOGRAPHY can also be done with interaction-free techniques. In this way, the object-a "Medusa" that must not be viewed directly-will absorb very few photons. |
Lying beyond the scope of everyday experience, the notion of interaction-
free measurements seems weird, if not downright nonsensical. Perhaps it would
seem less strange if one kept in mind that quantum mechanics operates in
the realm of potentialities. It is because there could have been an interaction
that we can prevent one from occurring.
If that does not help, take comfort in the fact that, over the years, even
physicists have had a hard time accepting the strangeness of the quantum
world. The underlying keys to these quantum feats of magic-the complementary,
wave- and-particle aspect of light and the nature of quantum measurements-have
been known since 1930. Only recently have physicists started to apply these
ideas to uncover new phenomena in quantum information processing, including
the ability to see in the dark.
The Authors
PAUL KWIAT, HARALD WEINFURTER and
ANTON ZEILINGER freely interacted with
one another at the University of Innsbruck. Kwiat, now a J. R. Oppenheimer
Fellow at Los Alamos National Laboratory, earned his Ph.D. from the University
of California, Berkeley. He is a serious student of aikido and is trying
to become a tolerable flautist. Weinfurter received his Ph.D. from the Technical
University of Vienna and held a postdoctoral position at the Hahn-Meitner
Institute in Berlin. He currently enjoys all the benefits and comforts of
a fellowship from the Austrian Academy of Science as well as the relaxing
lifestyle in Innsbruck and its surrounds. A member of the Austrian Academy
of Sciences, Zeilinger earned his doctorate at the University of Vienna and
has held numerous appointments worldwide. In his little free time, he plays
the double bass and collects antique maps, particularly of the Austro-Hungarian
empire. |
Further Reading
QED: THE STRANGE THEORY OF LIGHT AND MATTER. Richard P. Feynman.
Princeton University Press, 1985. |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |