Genetic Algorithms
Computer programs that "evolve" in ways that
resemble natural selection can
solve complex problems even
their creators do not fully understand
John H. Holland
| JOHN H. HOLLAND has been investigating the theory and practice of algorithmic evolution for nearly 40 years. He is a professor of psychology and of electrical engineering and computer science at the University of Michigan. Holland received a B.S. in physics from the Massachusetts Institute of Technology in 1950 and served on the Logical Planning Group for IBM's first programmed electronic computer (the 701) from 1950 until 1952. He received an M.A. in mathematics and a Ph-D. in communication sciences from the University of Michigan. Holland has been a member of the Steering Committee of the Santa Fe Institute since its inception in 1987 and is an external professor there. |
Living organisms are consummate problem solvers.They exhibit
a versatility that puts the best computer programs to shame.This observation
is especially galling for computer scientists, who may spend months or years
of intellectual effort on an algorithm, whereas
organisms come by their abilities through the
apparently undirected mechanism of evolution and natural selection.
Pragmatic researchers see evolution's remarkable power as
something to be emulated rather than envied. Natural selection eliminates
one of the greatest hurdles in software design: specifying in advance all
the features of a problem and the actions a program should take to deal with
them. By harnessing the mechanisms of evolution, researchers may be able
to "breed" programs that solve problems even when no person can fully understand
their structure. Indeed, these so-called genetic algorithms have already
demonstrated the ability to make breakthroughs in the design of such complex
systems as jet engines.
Genetic algorithms make it possible to explore a far greater
range of potential solutions to a problem than do conventional programs.
Furthermore, as researchers probe the natural selection of programs under
controlled and well-understood conditions, the practical results they achieve
may yield some insight into the details of how life and
intelligence
evolved in the natural world.
Most organisms evolve by means of two primary processes: natural
selection and sexual reproduction.The first determines which members of a
population survive to reproduce, and the second ensures mixing and recombination
among the genes of their offspring. When sperm and ova fuse, matching
chromosomes line up with one another and then
cross over partway along their length, thus swapping genetic material. This
mixing allows creatures to evolve much more rapidly than they would if each
offspring simply contained a copy of the genes of a single parent, modified
occasionally by mutation. (Although unicellular organisms do not engage in
mating as humans like to think of it, they do exchange genetic material,
and their evolution can be described in analogous terms.)
Selection is simple: if an organism fails some test of fitness,
such as recognizing a predator and fleeing, it dies. Similarly, computer
scientists have little trouble weeding out poorly performing algorithms.
If a program is supposed to sort numbers in ascending order, for example,
one need merely check whether each entry of the program's output is larger
than the preceding one.
People have employed a combination of crossbreeding and selection
for millennia to breed better crops, racehorses or ornamental roses. It is
not as easy, however, to translate these procedures for use on computer programs.
The chief problem is the construction of a "genetic
code" that can represent the structure of different programs, just as
DNA represents the structure of a person or a mouse.
Mating or mutating the text of a
FORTRAN program, for example, would in
most cases not produce a better or worse FORTRAN program but rather no program
at all.
The first attempts to mesh computer science and evolution,
in the late 1950s and early 1960s, fared poorly because they followed the
emphasis in biological texts of the time and relied on mutation rather than
mating to generate new gene combinations.Then, in the early 1960s, Hans J.
Bremermann of the University of California at Berkeley added a kind of mating:
the characteristics of offspring were determined by summing up corresponding
genes in the two parents. This mating procedure was limited, however, because
it could apply only to characteristics that could be added together in a
meaningful way.
During this time, I had been investigating mathematical analyses
of adaptation and had become convinced that the recombination of groups of
genes by means of mating was a critical part of evolution. By the mid-1960s
I had developed a programming technique, the genetic algorithm, that is well
suited to evolution by both mating and mutation. During the next decade,
I worked to extend the scope of genetic algorithms by creating a genetic
code that could represent the structure of any computer program.
The result was the classifier system, consisting of a set
of rules, each of which performs particular actions every time its conditions
are satisfied by some piece of information.The conditions and actions are
represented by strings of bits corresponding to the presence or absence of
specific characteristics in the rules' input and output For each characteristic
that was present, the string would contain a 1 in the appropriate position,
and for each that was absent, it would contain a 0. For example, a classifier
rule that recognized dogs might be encoded as a string containing 1's for
the bits corresponding to "hairy," "slobbers," "barks," "loyal" and "chases
sticks" and 0's for the bits corresponding to "metallic," "speaks Urdu" and
"possesses credit cards." More realistically, the programmer should choose
the simplest, most primitive characteristics so that they can be combined-as
in the game of 20 Questions-to classify a wide range of objects and
situations.
Although they excel at recognition, these rules can also be
made to trigger actions by tying bits in their output to the appropriate
behavior [see Illustration].
Any program that can be written in a standard programming language such as
FORTRAN or LISP can be rewritten as a classifier system.
To evolve classifier rules that solve a particular problem,
one simply starts with a population of random strings of 1's and 0's and
rates each string according to the quality of its result. Depending on the
problem, the measure of fitness could be business profitability, game payoff,
error rate or any number of other criteria. High-quality strings mate;
low-quality ones perish.As generations pass, strings associated with improved
solutions will predominate. Furthermore, the mating process continually combines
these strings in new ways, generating ever more sophisticated solutions.
The kinds of problems that have yielded to the technique range from developing
novel strategies in game theory to designing complex mechanical systems.
Recast in the language of genetic algorithms, the search for
a good solution to a problem is a search for particular binary strings. The
universe of all possible strings can be considered as an imaginary landscape;
valleys mark the location of strings that encode poor solutions, and the
landscape's highest point corresponds to the best possible string.
Regions in the solution space can also be defined by looking
at strings that have 1's or 0's in specified places-a kind of binary equivalent
of map coordinates. The set of all strings that start with a 1, for example,
constitutes a region in the set of possibilities. So do all the strings that
start with a 0 or that have a 1 in the fourth position, a 0 in the fifth
and a 1 in the sixth and so on.
 |
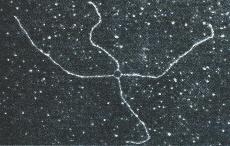
| BEE ORCHID demonstrates the specificity with which natural genetic selection can match an organism to a particular niche. The flower, which resembles a female bumblebee, is fertilized by male bees that attempt to mate with it. Mechanisms similar to natural selection, the author says, can produce computer programs (so-called genetic algorithms) capable of solving such complex problems as the design of jet engines or communications networks. |
One conventional technique for exploring such a landscape
is hill climbing: start at some random point, and if a slight modification
improves the quality of your solution, continue in that direction; otherwise,
go in the opposite direction. Complex problems, however, make landscapes
with many high points. As the number of dimensions of the problem space
increases, the countryside may contain tunnels, bridges and even more convoluted
topological features. Finding the right hill or even determining which way
is up becomes increasingly difficult. In addition, such search spaces are
usually enormous. If each move in a chess game,
for example, has an average of 10 alternatives, and a typical game lasts
for 30 moves on each side, then there are about 1060 strategies
for playing chess (most of them bad).
Genetic algorithms cast a net over this landscape. The multitude
of strings in an evolving population samples it in many regions simultaneously.
Notably the rate at which the genetic algorithm samples different regions
corresponds directly to the regions' average "elevation"-that is, the probability
of finding a good solution in that vicinity.
This remarkable ability of genetic algorithms to focus their
attention on the most promising parts of a solution space is a direct outcome
of their ability to combine strings containing partial solutions. First,
each string in the population is evaluated to determine the performance of
the strategy that it encodes. Second, the higher-ranking strings mate. Two
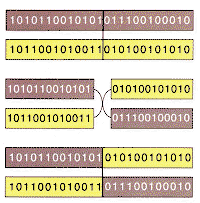
strings line up, a point along the strings is selected at random and the
portions to the left of that point are exchanged to produce two offspring:
one containing the symbols of the first string up to the crossover point
and those of the second beyond it, and the other containing the complementary
cross [see illustration below]. Biological chromosomes cross over
one another when two gametes meet to form a zygote, and so the process of
crossover in genetic algorithms does in fact closely mimic its biological
model. The offspring do not replace the parent strings; instead they replace
low-fitness strings, which are discarded at each generation so that the total
population remains the same size.
 |
|
|
| CROSSOVER is the fundamental mechanism of genetic rearrangement for both real organisms and genetic algorithms. | ||
Third, mutations modify a small fraction of the strings: roughly
one in every 10,000 symbols flips from 0 to 1, or vice versa. Mutation alone
does not generally advance the search for a solution, but it does provide
insurance against the development of a uniform population incapable of further
evolution.
The genetic algorithm exploits
the higher-payoff, or "target," regions of the solution space, because successive
generations of reproduction and crossover produce increasing numbers of strings
in those regions. The algorithm favors the fittest strings as parents, and
so above-average strings (which fall in target regions) will have more offspring
in the next generation.
Indeed, the number of strings in a given region increases
at a rate proportional to the statistical estimate of that region' s fitness.
A statistician would need to evaluate dozens of samples from thousands or
millions of regions to estimate the average fitness of each region. The genetic
algorithm manages to achieve the same result with far fewer strings and virtually
no computation.
The key to this rather surprising behavior is the fact that
a single string belongs to all the regions in which any of its bits appear.
For example, the string 11011001 is a member of regions 11****** (where the
* indicates that a bit's value is unspecified), 1******1 , **0**00* and so
forth. The largest regions-those containing many unspecified bits-will typically
be sampled by a large fraction of all the strings in a population. Thus,
a genetic algorithm that manipulates a population of a few thousand strings
actually samples a vastly larger number of regions. This implicit parallelism
gives the genetic algorithm its central advantage over other problem-solving
processes.
Crossover complicates the effects of implicit parallelism.
The purpose of crossing strings in the genetic algorithm is to test new parts
of target regions rather than testing the same string over and over again
in successive generations. But the process can also "move" an offspring out
of one region into another, causing the sampling rate of different regions
to depart from a strict proportionality to average fitness. That departure
will slow the rate of evolution.
The probability that the offspring of two strings will leave
its parents' region depends on the distance between the 1's and 0's that
define the region. The offspring of a string that samples 10****, for example,
can be outside that region only if crossover begins at the second position
in the string-one chance in five for a string containing six genes. (The
same building block would run a risk of only one in 999 if contained in a
1,000-gene string.) The offspring of a six-gene string that samples region
1****1 runs the risk of leaving its parents' region no matter where crossover
occurs.
Closely adjacent 1's or 0's that define a region are called
compact building blocks. They are most likely to survive crossover intact
and so be propagated into future generations at a rate proportional to the
average fitness of strings that carry them. Although a reproduction mechanism
that includes crossover does not manage to sample all regions at a rate
proportional to their fitness, it does succeed in doing so for all regions
defined by compact building blocks. The number of compactly defined building
blocks in a population of strings still vastly exceeds the number of strings,
and so the genetic algorithm still exhibits implicit parallelism.
Curiously, an operation in natural genetics called inversion
occasionally rearranges genes so that those far apart in the parents may
be placed close to one another in the offspring. This amounts to redefining
a building block so that it is more compact and less subject to being broken
up by crossover. If the building block specifies a region of high average
fitness, then the more compact version automatically displaces the less compact
one because it loses fewer offspring to copying error. As a result, an adaptive
system using inversion can discover and favor compact versions of useful
building blocks.
The genetic algorithm's implicit parallelism allows it to test
and exploit large numbers of regions in the search space while manipulating
relatively few strings. Implicit parallelism also helps genetic algorithms
to cope with nonlinear problems-those in which the fitness of a string containing
two particular building blocks may be much greater (or much smaller) than
the sum of the fitnesses attributable to each building block alone.
Linear problems present a reduced search space because the
presence of a 1 or a 0 at one position in a string has no effect on the fitness
attributable to the presence of a 1 or 0 somewhere else. The space of 1,000-digit
strings, for example, contains more than 31,000 possibilities,
but if the problem is linear, an algorithm need investigate only strings
containing 1 or 0 at each position, a total of just 2,000 possibilities.
When the problem is
nonlinear, the difficulty increases
sharply.The average fitness of strings in the region * 01***, for example,
could be above the population average, even though the fitnesses associated
with * 0**** and **1*** are below the population average. Nonlinearity does
not mean that no useful building blocks exist but merely that blocks consisting
of single 1's or 0's will be inadequate. That characteristic, in turn, leads
to an explosion of possibilities: the set of all strings 20 bits in length
contains more than three billion building blocks. Fortunately, implicit
parallelism can still be exploited. In a population of a few thousand strings,
many compact building blocks will appear in 100 strings or more, enough to
provide a good statistical sample. Building blocks that exploit nonlinearities
to attain above-average performance will automatically be used more often
in future generations.
In addition to coping with nonlinearity, the genetic algorithm
helps to solve a conundrum that has long bedeviled conventional problem-solving
methods: striking a balance between exploration and exploitation. Once one
finds a good strategy for playing chess, for example, it is possible to
concentrate on exploiting that strategy. But this choice carries a hidden
cost because exploitation makes the discovery of truly novel strategies unlikely.
Improvements come from trying new, risky things. Because many of the risks
fail, exploration involves a degradation of performance. Deciding to what
degree the present should be mortgaged for the future is a classic problem
for all systems that adapt and learn.
The genetic algorithm' s approach to this obstacle turns on crossover. Although crossover can interfere with the exploitation of a building block by breaking it up, this process of recombination tests building blocks in new combinations and new contexts. Crossover generates new samples of above-average regions, confirming or disproving the estimates produced by earlier samples. Furthermore, when crossover breaks up a building block, it produces a new block that enables the genetic algorithm to test regions it has not previously sampled.
The Prisoner's Dilemma |
||
| PLAYER | (B) COOPERATE |
(B) DEFECT |
| (B) COOPERATE |
3/3 |
5/0 |
| (B) DEFECT |
0/5 |
0/0 |
| IN PRISONER'S DILEMMA each player can either cooperate or defect and receives a payoff based on the other's choice. If both cooperate, for example, both receive three points. Mutual defection is the safest strategy, but repeated play often leads to cooperation instead. | ||
The game known as the Prisoner's
Dilemma [Ref: "The Politics of Private
Desire" M.Laver p47;Psychology Today
Aug96 p46] illustrates the genetic algorithm's ability to balance exploration
against exploitation. This long-studied game presents its two players with
a choice between "cooperation" and "defection": if both players cooperate,
they both receive a payoff; if one player defects, the defector receives
a higher payoff and the cooperator receives nothing; if both defect, they
both receive a minimal payoff [see table above]. For example, if player
A cooperates and player B defects, then player A receives no payoff and player
B receives a payoff of five points.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Political scientists and sociologists have studied the Prisoner's
Dilemma because it provides a simple, clear-cut example of the difficulties
of cooperation. Game theory predicts that each player should minimize the
maximum damage the other player can inflict: that is, both players should
defect.Yet when two people play the game together repeatedly, they typically
learn to cooperate with each other to raise their joint payoff. One of the
most effective known strategies for the Prisoner's Dilemma is "tit for tat,"
which begins by cooperating but thereafter mimics the last play of the other
player. That is, it "punishes" a defection by defecting the next time, and
it rewards cooperation by cooperating the next time.
Robert Axelrod of the University of Michigan, working with
Stephanie Forrest, now at the University of New Mexico, decided to find out
if the genetic algorithm could discover the tit-for-tat strategy. Applying
the genetic algorithm first requires translating possible strategies into
strings. One simple way is to base the next response on the outcome of the
last three plays. Each iteration has four possible outcomes, and so a sequence
of three plays yields 64 possibilities. A 64-bit string contains one gene
(or bit position) for each. The first gene, for instance, would be allocated
to the case of three consecutive mutual cooperations and the last to three
mutual defections. The value of each gene would be either 1 or 0 depending
on whether the preferred response to its corresponding history was cooperation
or defection. For example, the 64-bit string consisting of all 0's would
designate the strategy that defects in all cases. Even for such a simple
game, there are 264 (approximately 16 quadrillion) different
strategies.
Axelrod and Forrest supplied the genetic algorithm with a small
random collection of strings representing strategies. The fitness of each
string was simply the average of the payoffs its strategy received under
repeated play. All these strings had low fitnesses because most strategies
for playing the Prisoner's Dilemma are not very good. Quickly the genetic
algorithm discovered and exploited tit for tat, but further evolution introduced
an additional improvement.The new strategy, discovered while the genetic
algorithm was already playing at a high level, exploited players that could
be "bluffed"-lured into cooperating repeatedly in the face of defection.
It reverted to tit for tat, however, when the history indicated the player
could not be bluffed.
| GENE POOL of algorithms consists of strings of 1's and 0's. Each string is evaluated for fitness, and the best strings mate (second column) and produce offspring by means of crossover (indicated by a vertical black line). Strings of indeterminate fitness simply survive to the next generation, and the least fit perish. If particular patterns of bits (shown here by colored areas) improve the fitness of strings that carry them, repeated cycles of evaluation and mating (succeeding columns) will cause the proportion of these high-quality "building blocks" to increase. The pattern corresponding to each building block appears in the rightmost column; asterisks represent bits whose values are unspecified. |
Biological evolution operates, of course, not to produce a
single superindividual but rather to produce interacting species well adapted
to one another. (Indeed, in the biological realm there is no such thing as
a best individual.) Similarly, the genetic algorithm can be used, with
modifications, to govern the evolution not merely of individual rules or
strategies but of classifier-system "organisms" composed of many rules. Instead
of selecting the fittest rules in isolation, competitive pressures can lead
to the evolution of larger systems whose abilities are encoded in the strings
that make them up.
Re-creating evolution at this higher level requires several
modifications to the original genetic algorithm. Strings still represent
condition-action rules, and each rule whose conditions are met generates
an action as before. Rating each rule by the number of correct actions it
generates, however, will favor the evolution of individual "superrules" instead
of finding clusters of rules that interact usefully. To redirect the search
toward interacting rules, the procedure is modified by forcing rules to compete
for control of the system's actions. Each rule whose conditions are met competes
with all other rules whose conditions are met, and the strongest rules determine
what the system will do in that given situation. If the system's actions
lead to a successful outcome, all the winning rules are strengthened; otherwise
they are weakened.
Another way of looking at this method is to consider each rule
string as a hypothesis about the classifier's world. A rule enters the
competition only when it "claims" to be relevant to the current situation.
Its ability to compete depends on how much of a contribution it has made
to solving similar problems. As the genetic algorithm proceeds, strong rules
mate and form offspring rules that combine their parents' building blocks.
These offspring, which replace the weakest rules, amount to plausible but
untried hypotheses.
Competition among rules provides the system with a graceful
way of handling perpetual novelty. When a system has strong rules that respond
to a particular situation, that is the equivalent of saying that it has certain
well-validated hypotheses. Offspring rules, which begin life weaker than
do their parents, can win the competition and influence the system's behavior
only when there are no strong rules whose conditions are satisfied-in other
words, when the system does not know what to do. If their actions help, they
survive; if not, they are soon replaced. Thus, the offspring do not interfere
with the system's action in well- practiced situations but wait gracefully
in the wings as hypotheses about what to do under novel circumstances.
Adding competition in this way strongly affects the evolution
of a classifier system. Shortly after the system starts running, it evolves
rules with simple conditions-treating a broad range of situations as if they
were identical. The system exploits such rules as defaults that specify something
to be done in the absence of more detailed information. Because the default
rules make only coarse discriminations, however, they are often wrong and
so do not grow in strength. As the system gains experience, reproduction
and crossover lead to the development of more complex, specific rules that
rapidly become strong enough to dictate behavior in particular cases.
Eventually the system develops a hierarchy: layers of exception
rules at the lower levels handle most cases, but the default rules at the
top level of the hierarchy come into play when none of the detailed rules
has enough information to satisfy its conditions. Such default hierarchies
bring relevant experience to bear on novel situations while preventing the
system from becoming bogged down in overly detailed options.
The same characteristics that make evolving classifier systems
adept at handling perpetual novelty also do a good job of handling situations
where the payoff for a given action may come only long after the action is
taken. The earliest moves of a chess game, for example,
may set the stage for later victory or defeat.
To train a classifier system for such long-term goals, a programmer
gives the system a payoff each time it completes a task. The credit for success
(or the blame for failure) can propagate through the hierarchy to
strengthen (or
weaken) individual rules even if their actions had only a distant effect
on the outcome. Over the course of many generations the system develops rules
that act ever earlier to set the stage for later payoffs. It therefore becomes
increasingly able to anticipate the consequences of its actions.
Genetic algorithms have now been tested in a wide variety of
contexts. David E. Goldberg of the University of Illinois, for example, has
developed algorithms that learn to control a gas pipeline system modeled
on the one that carries natural gas from the Southwest to the Northeast.
The pipeline complex consists of many branches, all carrying various amounts
of gas; the only controls available are compressors that increase pressure
in a particular branch of the pipeline and valves to regulate the flow of
gas to and from storage tanks. Because of the tremendous lag between manipulating
valves or compressors and the actual pressure changes in the lines, there
is no analytic solution to the problem, and human controllers, like Goldberg's
algorithm, must learn by apprenticeship.
Goldberg's system not only met gas demand at costs comparable
to those achieved in practice, but it also developed a hierarchy of default
rules capable of responding properly to holes punched in the pipeline (as
happens all too often in reality at the blade of an errant bulldozer). Lawrence
Davis of Tica Associates in Cambridge, Mass., has used similar techniques
to design communications networks; his software's goal is to carry the maximum
possible amount of data with the minimum number of transmission lines and
switches interconnecting them.
A group of researchers at General Electric and Rensselaer
Polytechnic Institute recently put a genetic algorithm to good use in the
design of a high-by- pass jet engine turbine such as those that power commercial
airliners. Such turbines, which consist of multiple stages of stationary
and rotating blade rows enclosed in a roughly cylindrical duct, are at the
center of engine-development projects that last five years or more and consume
up to $2 billion.
The design of a turbine involves at least 100 variables, each
of which can take on a different range of values.The resulting search space
contains more than 10387 points. The "fitness" of the turbine
depends on how well it satisfies a series of 50 or so constraints, such as
the smooth shape of its inner and outer walls or the pressure, velocity and
turbulence of the flow at various points inside the cylinder. Evaluating
a single design requires running an engine simulation that takes about 30
seconds on a typical engineering workstation.
 |
| SOFTWARE TO DESIGN JET TURBINE includes a genetic algorithm that combines the best features of designs produced by other programs. Engineers using the algorithm achieved better results than with more conventional software aids. |
In one fairly typical case, an engineer working alone took
about eight weeks to reach a satisfactory design. So-called expert systems,
which use inference rules based on experience to predict the effects of a
change of one or two variables, can help direct the designer in seeking out
useful changes. An engineer using such an expert system took less than a
day to design an engine with twice the improvements of the eight-week manual
design.
Such expert systems, however, soon get stuck at points where
further improvements can be made only by changing many variables simultaneously.
These dead ends occur because it is practically impossible to sort out all
the effects associated with different multiple changes, let alone to specify
the regions of the design space within which previous experience remains
valid.
To get away from such a point, the designer must find new building
blocks for a solution. Here is where the genetic algorithm comes into play.
Seeding the algorithm with designs produced by the expert system, an engineer
took only two days to find a design with three times the improvements of
the manual version (and half again as many as using the expert system alone).
This example points up both a strength and a limitation of
simple genetic algorithms: they are at their best when exploring complex
landscapes to locate regions of enhanced opportunity. But if a partial solution
can be improved further by making small changes in a few variables, it is
best to augment the genetic algorithm with other, more standard methods.
Although genetic algorithms mimic the effects of natural selection,
until now they have operated on a much smaller scale than does biological
evolution. My colleagues and I have run classifier systems containing as
many as 8,000 rules, but this size is at the low end of viability for natural
populations. Large animals that are not endangered may number in the millions,
insect populations in the trillions and bacteria in the quintillions or more.
These large numbers greatly enhance the advantages of implicit parallelism.
As massively parallel computers become
more common, it will be feasible to evolve software populations whose size
more closely approaches those of natural species. Indeed, the genetic algorithm
lends itself nicely to such machines. Each processor can be devoted to a
single string because the algorithm's operations focus on single strings
or, at most, a pair of strings during crossover. As a result, the entire
population can be processed in parallel.
We still have much to learn about classifier systems, but the
work done so far suggests they will be capable of remarkably complex behavior.
Rick L. Riolo of the University of Michigan has
already observed genetic algorithms that display "latent learning" (a phenomenon
in which an animal such as a rat explores a maze without reward and is
subsequently able to find food placed in the maze much more quickly).
At the Santa Fe Institute, Forrest, W Brian Arthur, John H.Miller,
Richard G. Palmer and I have used classifier systems to simulate economic
agents of limited rationality. These agents evolve to the point of acting
on trends in a simple commodity market, producing
speculative bubbles and crashes.
The simulated worlds these agents inhabit show many similarities
to natural ecosystems: they exhibit counterparts to such phenomena as symbiosis,
parasitism, biological "arms races," mimicry, niche formation and speciation.
Still other work with
genetic
algorithms has shed light on the conditions under which evolution will
favor sexual or asexual reproduction. Eventually artificial adaptation may
repay its debt to nature by increasing researchers' understanding of natural
ecosystems and other complex adaptive systems.
| ** COMPUTER PROGRAM SPEEDS SEARCH FOR NOVEL ALLOYS Hundreds
of thousands of possible metal alloy combinations can be formed from a relatively
small number of elements. As a result, finding new metal blends with desirable
qualities (such as rust resistance or heat conductivity) can be an arduous
task. Now a team of Danish physicists has developed a novel approach to this
treasure hunt, using a computer algorithm that borrows from evolutionary
theory to test which compounds hold the most promise for resisting high
temperatures and corrosion.
http://sciam.rsc03.net/servlet/cc?lJpDUAVEmLtisHklLkpLlFHhsDJhtE0EB |